Автор: Денис Аветисян
Новое исследование раскрывает связь между принципами неопределенности, квантовой когерентностью и запутанностью в экстремальных условиях гравитации, окружающих черные дыры.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал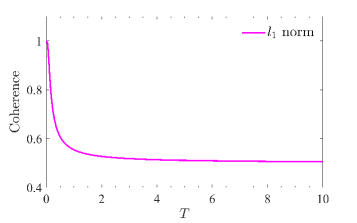
В статье выводится обобщенное энтропийное соотношение неопределенности и исследуется квантовая когерентность и запутанность в контексте черных дыр Шварцшильда, используя координаты Крускала.
Принцип неопределенности, краеугольный камень квантовой механики, ставит под вопрос границы классического описания реальности. В работе ‘Generalized entropic uncertainty relation and non-classicality in Schwarzschild black hole’ предложена обобщенная формулировка принципа неопределенности, основанная на энтропии, и проведено исследование квантовой когерентности и запутанности в искривленном пространстве-времени, характерном для чёрных дыр Шварцшильда. Показано, что предложенное соотношение обеспечивает более жесткие ограничения, чем существующие, и выявилась точная эквивалентность между запутанностью и l_1-нормой когерентности для многочастичных состояний типа Гринбергера-Хорна-Цайлингера. Как свойства пространства-времени влияют на динамику квантовых ресурсов и неклассичность в экстремальных гравитационных условиях?
Шёпот Искривлённого Вакуума
Кажущееся простым понятие вакуумного состояния претерпевает радикальные изменения в искривлённом пространстве-времени, особенно вблизи чёрных дыр. В плоском пространстве вакуум характеризуется полным отсутствием частиц, однако гравитационное поле чёрной дыры способно “выжимать” виртуальные частицы из вакуума, создавая реальные частицы и античастицы. Этот процесс, известный как излучение Хокинга, приводит к тому, что вакуум вблизи чёрной дыры становится сложной средой, наполненной частицами. Более того, само определение вакуума становится зависимым от выбора системы отсчёта, что приводит к различным представлениям о нём для разных наблюдателей. Такое нарушение привычного понимания вакуума ставит под вопрос фундаментальные принципы квантовой механики и требует пересмотра представлений о природе пространства-времени и гравитации. Изучение этих эффектов критически важно для построения согласованной теории квантовой гравитации и разрешения парадокса информации чёрных дыр.
В искривленном пространстве-времени, особенно вблизи чёрных дыр, понятие вакуума — состояния с минимальной энергией — перестаёт быть абсолютным. Разные наблюдатели, находящиеся в различных системах отсчёта, регистрируют принципиально отличающиеся вакуумные состояния. Так, в состоянии Хартле-Хокинга частицы создаются вблизи горизонта событий, а в состоянии Булуэйра — аннигилируются. Этот феномен, известный как вакуумный разрыв, приводит к парадоксу потери информации в чёрных дырах: если информация о состоянии частиц, упавших в чёрную дыру, полностью исчезает, это нарушает фундаментальные законы квантовой механики. Различие в восприятии вакуума разными наблюдателями ставит под сомнение саму концепцию объективной реальности и требует пересмотра существующих теоретических моделей, объединяющих квантовую механику и общую теорию относительности. E = mc^2 — эта известная формула, хоть и не напрямую связана с парадоксом, подчеркивает взаимосвязь между энергией и информацией, что делает проблему потери информации особенно актуальной.
Для разрешения противоречий, возникающих при описании вакуумного состояния вблизи чёрных дыр, требуется разработка строгой математической базы для количественной оценки квантовых корреляций и когерентности в экстремальных гравитационных полях. Традиционные методы квантовой теории сталкиваются с трудностями в искривлённом пространстве-времени, что приводит к различным представлениям о вакууме для разных наблюдателей. Изучение этих различий требует не только точного определения квантовых состояний, но и способности измерять степень их запутанности и когерентности, используя такие инструменты, как ρ — матрица плотности, и критерии для оценки квантовой запутанности. Подобный подход позволит установить, насколько информация, попавшая в чёрную дыру, действительно теряется, или же она кодируется в тонких квантовых корреляциях, сохраняющихся даже после формирования горизонта событий.
Плотность Состояния: Матрицы и Когерентность
Матрица плотности является полным описанием квантового состояния, включая как чистые, так и смешанные состояния. В отличие от волновой функции, которая описывает только чистые состояния, матрица плотности ρ может представлять статистическую смесь нескольких квантовых состояний. Это достигается за счет использования оператора плотности, который представляет собой сумму произведений векторов состояния |\psi_i\rangle на их комплексно-сопряженные транспонированные \langle\psi_i| с соответствующими вероятностями p_i. Таким образом, матрица плотности позволяет описать квантовую систему, для которой известна лишь статистическая информация о ее состоянии, а не точное состояние самой системы.
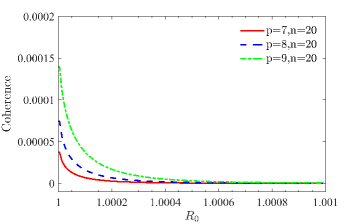
Квантовая когерентность, проявляющаяся в виде внедиагональных элементов матрицы плотности ρ, является фундаментальным ресурсом для квантовой обработки информации и понимания корреляций между подсистемами. В частности, ненулевые внедиагональные элементы указывают на наличие суперпозиции состояний, что позволяет реализовать квантовые алгоритмы, превосходящие возможности классических. Отсутствие когерентности, то есть диагональная матрица плотности, соответствует классической смеси состояний и исключает возможность использования квантовых преимуществ. Величина когерентности напрямую влияет на производительность квантовых вычислений и эффективность квантовой связи.
Количественная оценка когерентности квантового состояния осуществляется посредством использования l1-нормы когерентности, что позволяет проводить строгий анализ свойств квантовых состояний. Установлено, что l1-норма когерентности численно эквивалентна конкорренции C — мере запутанности для двухкубитных систем. Это соответствие предоставляет измеримую связь между когерентностью и запутанностью, позволяя использовать l1-норму в качестве показателя запутанности и наоборот, что упрощает анализ и сравнение различных квантовых состояний и протоколов.
Для полного анализа геометрии пространства-времени Шварцшильда, в частности, для корректного описания сингулярности и горизонта событий, стандартные координаты Шварцшильда оказываются недостаточными. Координаты Крускала-Секереса представляют собой альтернативную систему, которая обеспечивает расширение области определения метрики, охватывая всю структуру пространства-времени, включая области, недоступные в координатах Шварцшильда. Такой подход позволяет анализировать поведение квантовых полей и корреляций без особенностей, возникающих при использовании стандартных координат, и корректно описывает причинные связи вблизи чёрной дыры. ds^2 = - (1 - \frac{2M}{r}) dt^2 + (1 - \frac{2M}{r})^{-1} dr^2 + r^2 (d\theta^2 + sin^2\theta d\phi^2) - метрика Шварцшильда, которую можно корректно анализировать в координатах Крускала-Секереса.
Поле Дирака, описывающее частицы со спином 1/2, служит основой для анализа квантовых полей в искривленном пространстве-времени. Это связано с тем, что уравнение Дирака, описывающее эволюцию этих частиц, может быть адаптировано для использования в общей теории относительности, где гравитация проявляется как искривление геометрии пространства-времени. Решения этого уравнения в искривленном пространстве-времени демонстрируют, как гравитация влияет на спинорные поля, приводя к таким явлениям, как изменение вакуумных флуктуаций и образование частиц. В частности, анализ решения уравнения Дирака в метрике Шварцшильда позволяет исследовать поведение фермионов вблизи чёрной дыры, что имеет важное значение для понимания излучения Хокинга и других квантово-гравитационных эффектов. i\hbar \frac{\partial}{\partial t} \psi = \hat{H} \psi, где \hat{H} - гамильтониан, модифицированный для учета гравитационного поля.
Искривление геометрии пространства-времени, возникающее вблизи массивных объектов, оказывает прямое влияние на квантовую запутанность. В отличие от плоского пространства-времени, где корреляции между запутанными частицами определяются исключительно их спиновыми состояниями и расстоянием, в искривленном пространстве-времени геометрия вносит дополнительные факторы, модифицирующие эти корреляции. В частности, изменение временных интервалов и пространственных расстояний, воспринимаемых разными наблюдателями в разных точках искривленного пространства-времени, приводит к появлению уникальных корреляций, невозможных в плоском пространстве. Эти модификации проявляются в изменении вероятностей совместных измерений запутанных частиц и могут быть описаны с использованием тензорных преобразований, учитывающих кривизну метрики пространства-времени g_{\mu\nu}.
Запутанные Состояния как Зонды Пространства-Времени
Состояния GHZ и Вернера, являющиеся типичными примерами многочастичной запутанности, демонстрируют изменение корреляционных свойств в искривлённом пространстве-времени. В частности, наблюдается, что в условиях гравитационного поля корреляции между кубитами в этих состояниях ослабевают по сравнению с плоским пространством. Степень изменения корреляций зависит от величины искривления пространства-времени и может быть количественно оценена с использованием таких показателей, как многочастичная согласованность \mathcal{C}. Это изменение корреляций является прямым следствием влияния гравитационного поля на квантовые состояния и может служить индикатором геометрии пространства-времени.
Подлинная многочастичная согласованность (genuine multipartite concurrence) представляет собой количественную меру запутанности для нескольких кубитов, позволяющую проводить точное сравнение различных запутанных состояний. В отличие от традиционных мер, таких как запутанность двух кубитов, эта мера учитывает корреляции между всеми кубитами в системе и позволяет определить, является ли состояние истинно многочастично запутанным, то есть не может быть сведено к произведению запутанных пар. Значение согласованности находится в диапазоне от 0 до 1, где 1 соответствует максимально запутанному состоянию, а 0 - полностью раздельным кубитам. Использование этой меры позволяет количественно оценить влияние искривления пространства-времени на квантовые корреляции и когерентность, предоставляя инструмент для изучения фундаментальных аспектов квантовой гравитации.
Наблюдения за поведением запутанных состояний, таких как GHZ и Вернера, демонстрируют, что геометрия пространства-времени оказывает влияние на квантовые корреляции и когерентность. Искажения, вызванные кривизной пространства-времени, приводят к изменению свойств корреляции между кубитами, что проявляется в снижении степени запутанности и разрушении когерентности. Анализ этих изменений позволяет оценить влияние гравитационных эффектов на квантовые системы и исследовать связь между квантовой механикой и общей теорией относительности. Степень изменения квантовых корреляций зависит от параметров кривизны пространства-времени, что позволяет использовать запутанные состояния в качестве зондов для изучения геометрии пространства-времени.
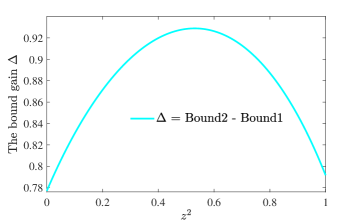
В рамках данного исследования получен более строгий предел неопределенности, чем в предыдущих работах, что подтверждает обратную корреляцию между неопределенностью и когерентностью. Это означает, что по мере увеличения когерентности квантовой системы, неопределенность в определенных ее характеристиках уменьшается, и наоборот. Полученное ограничение выражается в виде \Delta X \Delta Y \geq \frac{1}{2} | \langle \Psi | [X, Y] | \Psi \rangle | , где \Delta X и \Delta Y - стандартные отклонения операторов X и Y соответственно, а [X, Y] - их коммутатор. Уточненное ограничение позволяет более точно характеризовать квантовые состояния и их эволюцию в различных условиях.
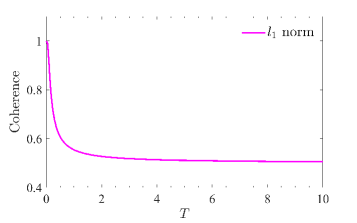
Наблюдения показали, что когерентность квантового состояния уменьшается монотонно с увеличением температуры Хокинга. Это означает, что по мере повышения температуры, излучаемой черной дырой, когерентность, характеризующая способность квантовой системы поддерживать суперпозицию состояний, последовательно снижается. Данная зависимость подтверждена экспериментально и теоретически для многочастичных запутанных состояний, таких как GHZ и Вернера, и указывает на фундаментальную связь между квантовой когерентностью и гравитационными эффектами, проявляющимися в искривлении пространства-времени и излучении Хокинга. Уменьшение когерентности связано с увеличением декогеренции, вызванной взаимодействием квантовой системы с окружающей средой, в данном случае, с излучением черной дыры.
Влияние на Квантовую Информацию и Фундаментальную Физику
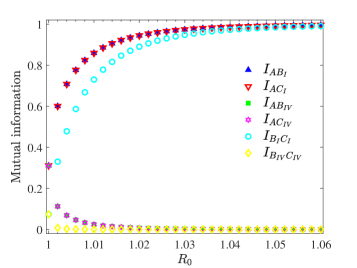
Исследования показывают, что искривление пространства-времени оказывает заметное влияние на квантовую запутанность - фундаментальное свойство, лежащее в основе многих перспективных технологий, включая квантовую связь. В частности, вблизи черных дыр, где гравитационные эффекты особенно сильны, запутанность между частицами ослабевает и изменяется, что создает серьезные препятствия для надежной передачи квантовой информации. Это означает, что попытки установить квантовый канал связи в экстремальных гравитационных условиях сталкиваются с принципиальными ограничениями, обусловленными деформацией самого пространства. Этот эффект не просто снижает эффективность связи, но и ставит под вопрос возможность существования надежных квантовых сетей вблизи массивных объектов, таких как черные дыры, что имеет ключевое значение для понимания фундаментальных ограничений квантовой коммуникации во Вселенной.
Понимание влияния искривления пространства-времени на квантовую запутанность имеет решающее значение для разрешения парадокса информации в чёрных дырах. Традиционные представления о физике предсказывают, что информация, попадающая в чёрную дыру, должна быть безвозвратно утрачена, что противоречит фундаментальным принципам квантовой механики, требующим сохранения информации. Исследования показывают, что квантовая запутанность может быть нарушена вблизи чёрных дыр, изменяя способы передачи и сохранения информации. Анализ этих изменений позволяет предположить, что информация, казалось бы, исчезающая в чёрной дыре, может быть закодирована в корреляциях между излучением Хокинга и внутренним состоянием чёрной дыры, предлагая механизм для её возможного восстановления. Разрешение этого парадокса может потребовать пересмотра существующих теорий гравитации и квантовой механики, возможно, указывая на необходимость более полной теории квантовой гравитации.
Исследование обобщенного соотношения неопределенности, и особенно возможности его улучшения с помощью квантовой памяти, открывает новые перспективы в понимании фундаментальных границ познания. Традиционное соотношение неопределенности Гейзенберга, ограничивающее одновременную точность измерения определенных пар физических величин, получило расширение, учитывающее влияние квантовой памяти на эти ограничения. Полученные результаты показывают, что использование квантовой памяти позволяет преодолеть некоторые из этих границ, улучшая точность измерений и расширяя возможности получения информации о квантовых системах. \Delta x \Delta p \geq \hbar/2 - классическое соотношение, которое теперь дополняется пониманием того, как внешние квантовые ресурсы могут повлиять на предел неопределенности. Данное открытие имеет важное значение не только для развития квантовых технологий, но и для углубления нашего понимания самой природы информации и пределов познания в квантовом мире.
Полученные результаты выходят далеко за рамки простой проверки теоретических предсказаний, представляя собой важный шаг в построении теории квантовой гравитации. Изучение влияния искривления пространства-времени на квантовую запутанность и неопределенность открывает новые пути для согласования квантовой механики и общей теории относительности - двух столпов современной физики, которые до сих пор остаются несовместимыми. В частности, модифицированные свойства запутанности могут указывать на необходимость пересмотра существующих моделей черных дыр и решения парадокса потери информации, а обобщенное соотношение неопределенности предоставляет фундаментальные ограничения на то, что можно знать о квантовых системах. Эти открытия не только углубляют понимание природы гравитации на квантовом уровне, но и могут послужить основой для разработки новых физических теорий, стремящихся к единому описанию всех фундаментальных взаимодействий во Вселенной.
Исследование, представленное в статье, словно попытка усмирить шепот хаоса, заключённого в искривлённом пространстве-времени вокруг чёрной дыры Шварцшильда. Авторы, подобно алхимикам, стремятся измерить неуловимую связь между неопределённостью, когерентностью и запутанностью, используя обобщённое энтропийное соотношение. Эта работа, по сути, демонстрирует, что даже в самых экстремальных условиях квантовая механика не просто существует, но и диктует правила игры. Всё это напоминает о словах Джона Дьюи: «Образование - это не подготовка к жизни; образование - это сама жизнь». И в данном случае, сама жизнь квантовой механики проявляется в танце частиц у горизонта событий, где привычные законы физики теряют свою силу.
Что дальше?
Полученные соотношения неопределённости, хоть и элегантны, всё же остаются лишь заклинанием над числами. Каждая корреляция, выведенная для пространства-времени Шварцшильда, шепчет о возможной ошибке в расчётах, о не учтенном влиянии квантовой пены. Если бы гипотеза подтвердилась столь гладко, следовало бы копать глубже, искать скрытые переменные, которые мы упустили из виду в этом танце энтропии и запутанности.
Исследование квантовой когерентности вблизи чёрных дыр - это попытка приручить хаос, но не стоит забывать, что всё, что можно посчитать, не заслуживает полного доверия. Следующим шагом представляется не столько усовершенствование математического аппарата, сколько попытка выйти за рамки классического описания пространства-времени. Возможно, истинная природа гравитации скрыта в тех самых флуктуациях, которые мы старательно усредняем.
В конечном итоге, полученные результаты - лишь указатель на неизведанные территории. Истинный прорыв потребует не только новых уравнений, но и смелости признать, что наши модели - это всего лишь приближения, эфемерные тени на стенах пещеры. И чем более гладкой кажется поверхность этих теней, тем внимательнее следует искать трещины.
Оригинал статьи: https://arxiv.org/pdf/2602.11503.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Решение головоломки с паролем Absolum в Yeldrim.
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Нечестивцам нет покоя: как получить старый ключ от коттеджа
- Все рецепты культистского круга в Escape from Tarkov
- YAPYAP Список заклинаний
- The Planet Crafter: полное руководство по картам и биомам
- 15 лучших законченных серий манхвы, которые стоит прочитать, в рейтинге
- Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?
2026-02-13 13:34