Тень темной материи: как гало из темной материи меняет поведение черных дыр

Автор: Денис Аветисян

Новое исследование показывает, как наличие гало из темной материи влияет на геометрию пространства-времени вокруг черной дыры Шварцшильда, изменяя траектории частиц и процессы излучения.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал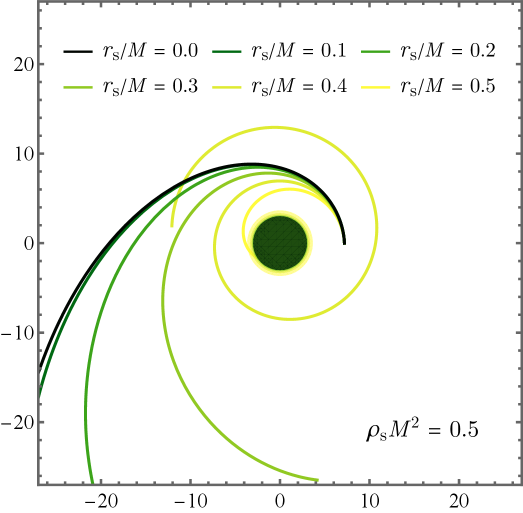

Траектории массивных частиц в искривлённом пространстве-времени чёрной дыры, погружённой в гало из тёмной материи Эрнквиста, демонстрируют зависимость от масштаба радиуса при плотности 0.5, раскрывая сложную динамику гравитационного взаимодействия в данной астрофизической среде.

В работе проведено исследование влияния гало из темной материи Эрнквиста на геодезические, рассеяние и поглощение частиц вблизи черной дыры Шварцшильда.

Несмотря на успешность общей теории относительности, влияние темной материи на гравитационные объекты остается предметом активных исследований. В данной работе, озаглавленной ‘Particle production, absorption, scattering, and geodesics in a Schwarzschild—Hernquist black hole’, проводится анализ квантовых и классических эффектов, возникающих вблизи черной дыры Шварцшильда, окруженной гало из темной материи по модели Эрнквиста. Полученные результаты демонстрируют, что присутствие гало влияет на процессы рождения частиц, поглощения и рассеяния скалярных волн, а также на геодезические траектории, изменяя характеристики излучения Хокинга и параметры испарения черной дыры. Каким образом модифицированная структура пространства-времени, обусловленная темной материей, повлияет на эволюцию и конечное состояние черных дыр в реальной Вселенной?

Ткань Пространства-Времени и Тёмная Материя: Зарождение Сцены

Понимание взаимодействия чёрных дыр напрямую зависит от точного определения геометрии окружающего их пространства-времени. Эта геометрия, описываемая метрикой пространства-времени, не является статичной, а искривляется массой чёрной дыры, определяя траектории движения света и материи в её окрестностях. Изучение этой искривлённости требует использования общей теории относительности Эйнштейна, где гравитация рассматривается не как сила, а как проявление геометрии пространства-времени. Точное определение метрики позволяет предсказывать такие явления, как гравитационное линзирование, смещение красного спектра и даже существование горизонтов событий. Любые отклонения в определении геометрии пространства-времени могут привести к неверным выводам о поведении чёрных дыр и окружающих их объектах. $g_{\mu\nu}$ тензор метрики, описывающий эту геометрию, является ключевым инструментом для моделирования и анализа гравитационных взаимодействий.

Метрика Шварцшильда, являющаяся краеугольным камнем в описании геометрии пространства-времени вокруг невращающейся чёрной дыры, предоставляет фундаментальную, но упрощённую модель. Однако, наблюдаемая Вселенная далека от идеальной изоляции: галактики и скопления галактик, окружающие чёрные дыры, насыщены тёмной материей. Учёт распределения этой невидимой субстанции становится критически важным для построения реалистичных моделей. Тёмная материя, оказывая гравитационное влияние, искажает геометрию пространства-времени, модифицируя траектории света и частиц, и, следовательно, изменяя поведение чёрной дыры. Поэтому, для точного предсказания эволюции чёрных дыр и понимания астрофизических процессов, происходящих в их окрестностях, необходимо включать в рассмотрение вклад тёмной материи и соответствующие модификации метрики пространства-времени.

Профиль плотности тёмной материи, описываемый гало Эрнквиста, предоставляет физически обоснованный подход к моделированию её влияния на геометрию пространства-времени вокруг чёрных дыр. В отличие от упрощённых моделей с однородным распределением, гало Эрнквиста предполагает, что плотность тёмной материи убывает с увеличением расстояния от центра, следуя степенному закону. $\rho(r) \propto \frac{1}{r^γ(1 + r/a)^γ}$ , где γ и $a$ — параметры, определяющие форму и масштаб распределения. Этот профиль хорошо соответствует результатам N-body симуляций формирования структуры во Вселенной и позволяет более реалистично учитывать гравитационное воздействие тёмной материи на движение объектов, включая чёрные дыры, и на распространение света вблизи них. Использование гало Эрнквиста позволяет исследователям создавать более точные модели, описывающие взаимодействие чёрных дыр и тёмной материи, что важно для понимания эволюции галактик и крупномасштабной структуры Вселенной.

Определение комбинированной метрики пространства-времени имеет первостепенное значение для точного прогнозирования поведения чёрных дыр. В то время как решение Шварцшильда описывает простейшую ситуацию, реальные астрофизические сценарии требуют учета распределения темной материи, оказывающей гравитационное влияние на окружающее пространство. Комбинированная метрика, учитывающая как гравитацию чёрной дыры, так и вклад темной материи, позволяет моделировать деформацию пространства-времени более реалистично. Точность этой метрики напрямую влияет на предсказания относительно движения частиц и света вблизи чёрной дыры, а также на анализ гравитационных волн, возникающих при взаимодействии чёрных дыр. $g_{\mu\nu}$ — компонент этой метрики, описывающий геометрию пространства-времени, — становится ключевым инструментом для понимания динамики чёрных дыр в сложных астрофизических условиях, позволяя исследователям создавать более точные модели и проверять теоретические предсказания.

Траектории фотонов вокруг черной дыры в гало из темной материи Хернквиста демонстрируют зависимость от параметра плотности при фиксированном радиусе масштаба в единицах массы, равном 0.5.

Распространение Поля и Радиальное Уравнение: Эхо в Искривлённом Пространстве

Для исследования взаимодействий рассматривается безмассовое скалярное поле, эволюция которого описывается волновым уравнением в заданном пространстве-времени. Данное уравнение имеет вид $\nabla^2 \phi - \frac{1}{c^2} \frac{\partial^2 \phi}{\partial t^2} = 0$ , где φ представляет собой скалярное поле, а $c$ — скорость света. Выбор безмассового поля упрощает анализ, позволяя сосредоточиться на динамике поля, определяемой метрикой пространства-времени. Волновое уравнение является фундаментальным в теории поля и описывает распространение возмущений в пространстве-времени.

Применение разделяемого анзаца (separable ansatz) позволяет упростить решение волнового уравнения для безмассового скалярного поля в искривленном пространстве-времени. Суть метода заключается в предположении, что поле можно представить в виде произведения функций, зависящих только от времени и только от пространственных координат. В частности, в сферически-симметричном случае, анзац имеет вид $\Psi(t,r,\theta,\phi) = R(r)Y(r,\theta,\phi)$ , где $R(r)$ — радиальная функция, описывающая зависимость поля от расстояния $r$ , а $Y(r,\theta,\phi)$ — сферическая гармоника, учитывающая угловую зависимость. Разделение переменной позволяет свести исходное уравнение в частных производных к одному обыкновенному дифференциальному уравнению для радиальной функции $R(r)$ , что значительно упрощает анализ и поиск решений.

Радиальное уравнение описывает эволюцию скалярного поля в зависимости от расстояния от центра рассматриваемой системы. Оно является следствием применения метода разделения переменных к волновому уравнению, применимому к безмассовому скалярному полю в заданной геометрии пространства-времени. Уравнение представляет собой дифференциальное уравнение второго порядка, решение которого определяет амплитуду поля как функцию радиуса $r$ . Форма уравнения зависит от метрики пространства-времени и, в частности, учитывает влияние кривизны пространства-времени и, если применимо, профиля гало темной материи, определяя, как поле распространяется и изменяется с увеличением расстояния от источника.

Эффективный потенциал в радиальном уравнении представляет собой ключевой элемент, отражающий комбинированное влияние искривления пространства-времени и гало темной материи на поведение скалярного поля. Он формируется путем добавления к гравитационному потенциалу, обусловленному метрикой пространства-времени $g_{\mu\nu}$ , вклада, описывающего распределение темной материи в гало. Математически, это выражается в виде потенциальной энергии, действующей на поле, и учитывает как геометрию пространства, так и гравитационное воздействие невидимой массы. Форма эффективного потенциала определяет возможные моды возбуждения поля и, следовательно, характеристики распространения волн в данном пространстве-времени с учетом присутствия темной материи.

Зависимость полного сечения рассеяния от частоты для чёрной дыры Хернста показывает, что при фиксированном <span class="katex-eq" data-katex-display="false">M\omega=3</span>, изменение параметра плотности <span class="katex-eq" data-katex-display="false">\rho\_{\text{s}}M^{2}</span> (при <span class="katex-eq" data-katex-display="false">r\_{\text{s}}/M=0.5</span>) и масштабированного радиуса <span class="katex-eq" data-katex-display="false">r\_{\text{s}}/M</span> (при <span class="katex-eq" data-katex-display="false">\rho\_{\text{s}}M^{2}=0.5</span>) существенно влияет на рассеяние. — Зависимость полного сечения рассеяния от частоты для чёрной дыры Хернста показывает, что при фиксированном $M\omega=3$ , изменение параметра плотности $\rho\_{\text{s}}M^{2}$ (при $r\_{\text{s}}/M=0.5$ ) и масштабированного радиуса $r\_{\text{s}}/M$ (при $\rho\_{\text{s}}M^{2}=0.5$ ) существенно влияет на рассеяние.

Граничные Условия и Анализ Рассеяния: Эхо в Безбрежной Пустоте

Физически корректные решения радиального уравнения должны удовлетворять определенным граничным условиям. Вблизи горизонта событий необходимо требовать существования только входящих волн, что соответствует отсутствию отражений и обеспечивает конечность физических величин. На бесконечности, напротив, решение должно представлять собой суперпозицию падающей и отраженной волн, описывающих взаимодействие поля с чёрной дырой. Математически это выражается требованием, чтобы решение имело форму $\Psi(r) \sim e^{-ik r} + Re^{-ik r}$ при $r \rightarrow \in fty$ , где $k$ — волновое число, а $R$ — коэффициент отражения. Выбор этих граничных условий критически важен для однозначного определения решения радиального уравнения и корректного расчета коэффициентов отражения и прохождения.

Условия на границе, а именно чисто входящие волны на горизонте событий и суперпозиция входящей и отраженной волн на бесконечности, однозначно определяют вид коэффициентов отражения $R$ и прохождения $T$ . Коэффициент отражения $R$ характеризует долю падающего поля, которое отражается от черной дыры, в то время как коэффициент прохождения $T$ определяет долю поля, которая проходит сквозь черную дыру или поглощается ею. Форма этих коэффициентов зависит от частоты падающего поля и параметров черной дыры, и именно они определяют, как поле рассеивается при взаимодействии с чёрной дырой, формируя характерную картину рассеяния.

Сдвиг фазы, возникающий в процессе рассеяния, является ключевым параметром, характеризующим взаимодействие поля с чёрной дырой. Он представляет собой изменение фазы рассеянной волны по отношению к падающей волне и напрямую связан с амплитудой рассеяния. Значение сдвига фазы зависит от энергии падающей волны и параметров чёрной дыры, таких как масса и спин. Анализ сдвига фазы позволяет определить, как поле взаимодействует с гравитационным полем чёрной дыры, и является важным инструментом при расчете коэффициентов отражения и прохождения, а также при определении сечения рассеяния и поглощения. $\delta(k)$ — стандартное обозначение сдвига фазы, зависящего от волнового числа $k$ .

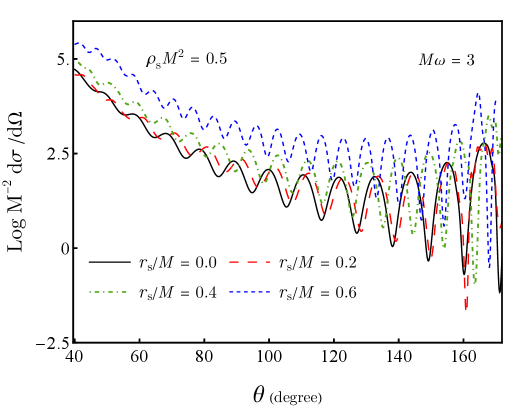
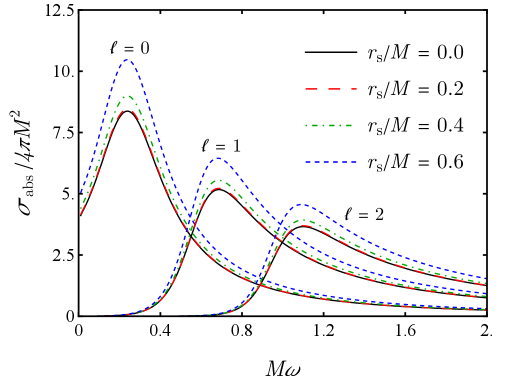
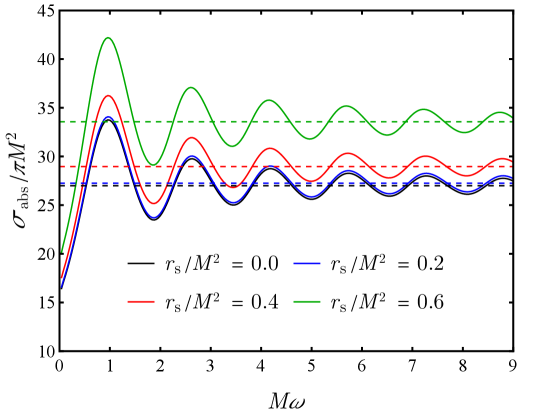
Использование разложения по частным волнам позволяет вычислить дифференциальное сечение рассеяния и сечение поглощения, количественно определяющие вероятности рассеяния и поглощения. Анализ показывает, что масштабный радиус $r_s/M$ оказывает более значительное влияние на эти сечения, чем параметр плотности $\rho_sM^2$ . Это означает, что размер горизонта событий, относительно массы черной дыры, является определяющим фактором в процессах рассеяния и поглощения, в большей степени, чем плотность вещества на горизонте событий.

Зависимость частичного сечения поглощения от <span class="katex-eq" data-katex-display="false">M\omega</span> для <span class="katex-eq" data-katex-display="false">\ell=0,1,2</span> демонстрирует, что изменение параметров Эрнквиста <span class="katex-eq" data-katex-display="false">r_s/M</span> и <span class="katex-eq" data-katex-display="false">\rho_s M^2</span> существенно влияет на поглощение, как показано на графиках с фиксированными значениями одного из параметров. — Зависимость частичного сечения поглощения от $M\omega$ демонстрирует, что при фиксированном нормализованном радиусе $r_{\text{s}}/M = 0.1$ (слева) или фиксированной плотности $\rho_{\text{s}}M^{2} = 0.1$ (справа) наблюдается соответствие между общим сечением поглощения и геометрическим сечением (обозначено штриховыми линиями).

Геодезическое Движение и Излучение Хокинга: Ткань Пространства-Времени Под Прессом

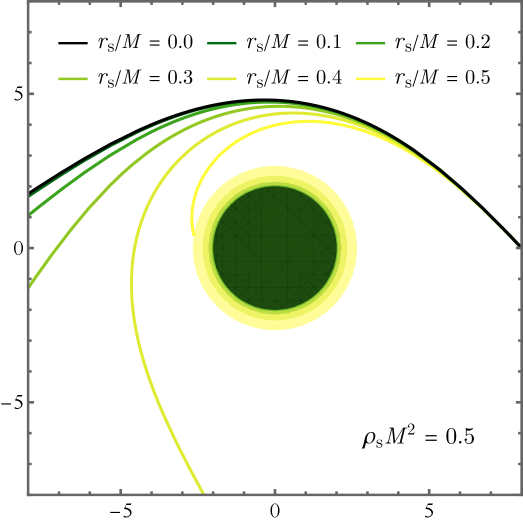
Для полного понимания поведения частиц и света вблизи чёрных дыр необходимо детальное изучение геодезических движений. Геодезические — это кратчайшие пути в искривленном пространстве-времени, определяемые гравитацией. Анализ этих траекторий позволяет предсказать, как объекты будут двигаться под влиянием огромной гравитационной силы чёрной дыры. Различные типы геодезических, такие как нулевые (для фотонов) и времениподобные (для массивных частиц), описывают разные сценарии движения, позволяя построить полную картину орбитального поведения и взаимодействия с чёрной дырой. Именно геодезические движения служат основой для понимания таких явлений, как гравитационное линзирование и аккреционные диски, а также для изучения более экзотических эффектов, таких как излучение Хокинга.

Движение частиц и света вблизи чёрных дыр описывается геодезическими линиями — кратчайшими путями в искривлённом пространстве-времени. Математически это описывается геодезическим уравнением, которое учитывает кривизну пространства-времени посредством символов Кристоффеля. Эти символы, являющиеся производными метрического тензора, отражают, как искривление пространства-времени влияет на траекторию движущихся объектов. Решение этого уравнения позволяет точно предсказать поведение как массивных частиц, движущихся по времениподобным геодезическим, так и безмассовых частиц, следующих по нулевым геодезическим. Таким образом, символы Кристоффеля выступают ключевым элементом, связывающим геометрию пространства-времени с динамикой частиц в гравитационном поле, определяя их отклонение от прямолинейного движения в плоском пространстве.

Для полного понимания движения объектов вблизи черных дыр необходимо учитывать как нулевые геодезические, описывающие траектории безмассовых частиц, таких как фотоны, так и времениподобные геодезические, определяющие движение массивных тел. Анализ нулевых геодезических позволяет исследовать распространение света и формирование структур, таких как фотонный диск, а изучение времениподобных геодезических раскрывает особенности орбит планет или звезд, находящихся под гравитационным влиянием черной дыры. Совместное рассмотрение этих двух типов геодезических обеспечивает целостную картину гравитационного взаимодействия и позволяет предсказать поведение различных объектов в экстремальных условиях сильного гравитационного поля. Именно комплексный подход, учитывающий как безмассовые, так и массивные частицы, необходим для построения адекватных моделей и интерпретации наблюдаемых астрономических явлений.

Предсказанное излучение Хокинга, изученное с использованием координат, таких как координаты Пайнлеве-Гулстранда, приводит к уменьшению массы чёрной дыры, что, в свою очередь, влияет на её остаточную массу. Расчеты показали, что температура Хокинга выражается формулой $1/(8πM) + (-Mr³s - r⁴s)ρsM/(2M + rs)²$ , что демонстрирует отклонение от чисто теплового профиля, характерного для геометрии Шварцшильда. Для обеспечения положительной остаточной массы, которая рассчитывается как $πρsrs³ + πρsrs² - rs$ , параметры модели были ограничены. Эти ограничения необходимы для предотвращения коллапса остаточной массы в отрицательные значения, что позволило получить более точные предсказания об эволюции чёрных дыр и их конечном состоянии.

Зависимость полного сечения поглощения от <span class="katex-eq" data-katex-display="false">M\omega</span> демонстрирует, что при фиксированном нормализованном радиусе <span class="katex-eq" data-katex-display="false">r_{\text{s}}/M = 0.1</span> (слева) или фиксированной плотности <span class="katex-eq" data-katex-display="false">\rho_{\text{s}}M^{2} = 0.1</span> (справа) наблюдается соответствие между общим сечением поглощения и геометрическим сечением (обозначено штриховыми линиями). — Зависимость полного сечения поглощения от $M\omega$ демонстрирует, что при фиксированном нормализованном радиусе $r_{\text{s}}/M = 0.1$ (слева) или фиксированной плотности $\rho_{\text{s}}M^{2} = 0.1$ (справа) наблюдается соответствие между общим сечением поглощения и геометрическим сечением (обозначено штриховыми линиями).

Исследование влияния тёмной материи на пространство-время вокруг чёрной дыры, предпринятое в данной работе, неизбежно подводит к пониманию системной взаимосвязанности всего сущего. Подобно тому, как гравитация искривляет свет, так и кажущиеся независимыми компоненты системы, такие как частицы и геодезические, оказывают влияние друг на друга. Как заметил Альбер Камю: «Всё стремится к зависимости». И действительно, анализ процессов поглощения и рассеяния частиц, а также исследование движения вдоль геодезических, демонстрируют, что даже вблизи чёрной дыры, где доминируют гравитационные силы, система проявляет признаки сложной, взаимосвязанной экосистемы. Каждый архитектурный выбор в моделировании, будь то параметры тёмного гало или условия на границе, предсказывает будущий сбой, отражая неизбежность системной зависимости.

Что дальше?

Исследование, представленное в данной работе, лишь приоткрывает завесу над тем, как плотное окружение темной материи влияет на поведение чёрных дыр. Анализ, опирающийся на частичные волны и геодезические линии, неизбежно наталкивается на границы применимости используемых упрощений. Каждое вычисленное сечение поглощения и рассеяния — это, скорее, пророчество о будущей погрешности, чем окончательный ответ. В конце концов, любая модель — это лишь эхо реальности, и эхо это с каждой итерацией становится всё более причудливым.

Следующим шагом видится отказ от строгих сферических симметрий. Реальные гало из темной материи далеки от идеальной гладкости, и их неоднородности, несомненно, вносят свой вклад в динамику окрестностей чёрной дыры. Изучение этих возмущений потребует новых математических инструментов и, возможно, откажется от аналитических решений в пользу численного моделирования. Каждый рефакторинг начинается как молитва и заканчивается покаянием, и так будет всегда.

Более того, данная работа оперирует с классическим и квантовым описаниями частиц, не затрагивая более глубокие вопросы о природе темной материи. Влияет ли темная материя на квантовое поле вокруг чёрной дыры? Возникают ли новые виды частиц в этих экстремальных условиях? Эти вопросы, вероятно, останутся открытыми на долгие годы, напоминая о том, что система — это не инструмент, а экосистема. Её нельзя построить, только взрастить, наблюдая за тем, как она просто взрослеет.

Оригинал статьи: https://arxiv.org/pdf/2602.15420.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-18 16:43