Тень у Черной Дыры: Новые Подходы к Поиску Экзотических Объектов

Автор: Денис Аветисян

---

Исследование показывает, как окружение черной дыры — темная материя и струнные облака — может повлиять на ее наблюдаемые характеристики, предлагая новые пути для ее идентификации.

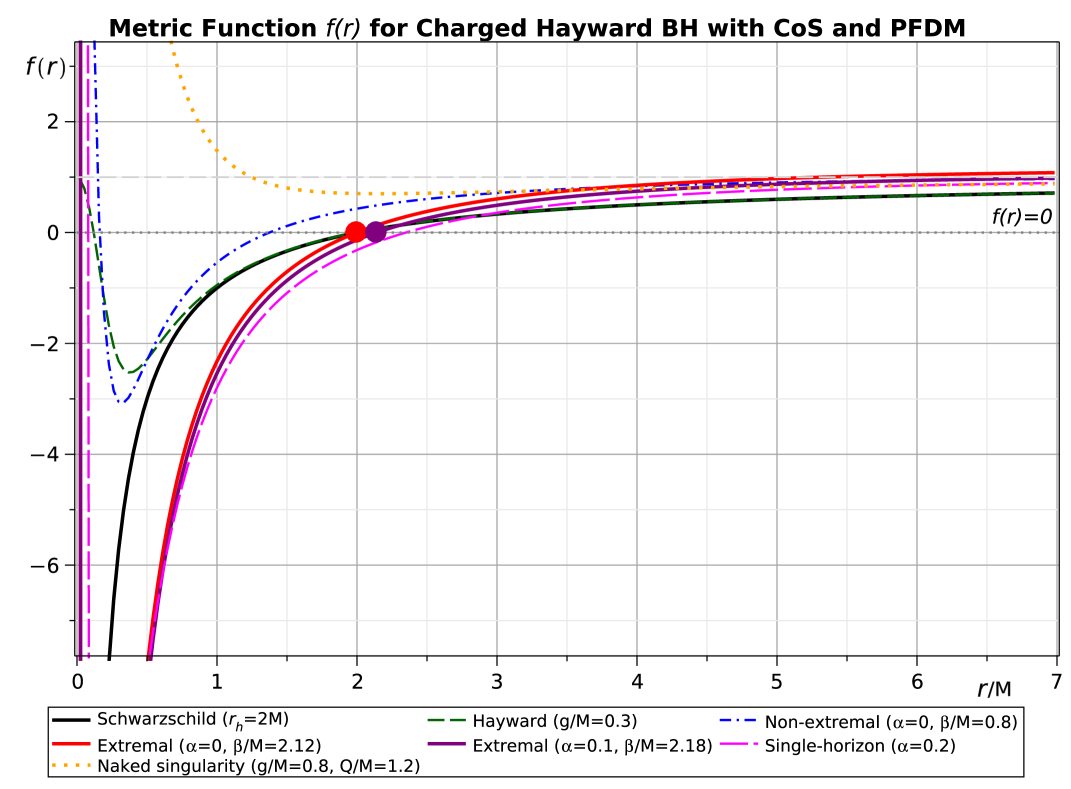
В работе анализируются свойства заряженной черной дыры Хейварда в среде темной материи и струнных облаков посредством изучения ее тени, геодезических и квазинормальных мод.

Несмотря на успехи общей теории относительности, применительно к описанию черных дыр, остаются вопросы о физической состоятельности сингулярностей и возможности их разрешения в рамках альтернативных моделей. В работе ‘Probing the Charged Hayward Black Hole in Dark Matter and String Cloud Environments through Shadow, Geodesics, and Quasinormal Spectrum’ исследуется геометрия заряженной черной дыры Хейварда, окруженной темной материей и облаком струн, с целью выявления наблюдаемых эффектов, отличающих её от классических решений. Показано, что параметры темной материи и облака струн оказывают заметное влияние на теневой радиус, геодезические и квазинормальные моды, позволяя потенциально ограничить их значения по астрономическим наблюдениям. Какие новые возможности для проверки моделей регулярных черных дыр открываются с развитием гравитационно-волновой астрономии и прецизионных измерений теней черных дыр?

---

За гранью метрики Шварцшильда: заряженная чёрная дыра Хейварда

Классические решения уравнений гравитации, такие как метрика Шварцшильда, несмотря на свою историческую значимость, сталкиваются с фундаментальными проблемами. В центре этих решений лежит сингулярность — точка, где плотность и кривизна пространства-времени становятся бесконечными, что противоречит физической реальности. Кроме того, эти модели не учитывают электрический заряд, который, как предполагается, может присутствовать у астрофизических черных дыр. Отсутствие реалистичного представления заряда ограничивает возможности использования этих решений для описания реальных объектов во Вселенной и требует разработки альтернативных подходов, способных преодолеть эти ограничения и обеспечить более адекватное описание экстремальных гравитационных полей. R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4}T_{\mu\nu}

Заряженная чёрная дыра Хейварда представляет собой значительный шаг вперед в понимании гравитации, предлагая регулярное решение уравнений Эйнштейна, которое избегает сингулярности, присущей классическому решению Шварцшильда. В отличие от последних, где плотность и кривизна пространства-времени стремятся к бесконечности в центре чёрной дыры, модель Хейварда предполагает конечное значение этих величин, что соответствует более реалистичному физическому сценарию. Ключевым отличием является введение параметра длины l, который эффективно “размывает” сингулярность, заменяя ее областью с конечной, хотя и экстремальной, плотностью. Такой подход не только устраняет математические проблемы, связанные с бесконечностями, но и позволяет исследовать физические процессы, происходящие вблизи горизонта событий, без столкновения с нефизическими результатами, что делает данную модель ценным инструментом для изучения сильной гравитации и альтернативных теорий гравитации.

Изучение пространства-времени, описываемого заряженной чёрной дырой Хейварда, имеет первостепенное значение для углубленного понимания сильной гравитации. В отличие от классических решений, таких как метрика Шварцшильда, данная модель позволяет исследовать гравитационные явления в экстремальных условиях, избегая сингулярностей и предоставляя более реалистичное представление о структуре чёрных дыр. Это, в свою очередь, открывает возможности для проверки и уточнения общей теории относительности, а также для исследования альтернативных теорий гравитации, которые могут описывать Вселенную в масштабах, недоступных для текущих моделей. Понимание свойств данного пространства-времени позволяет разрабатывать новые методы для изучения астрофизических процессов, происходящих вблизи чёрных дыр, и может привести к революционным открытиям в области космологии и фундаментальной физики. R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4}T_{\mu\nu}

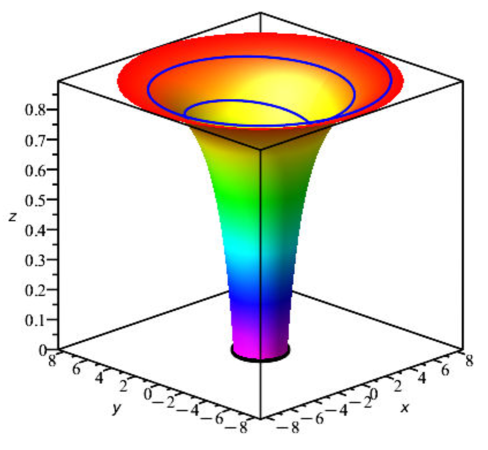
Тень чёрной дыры: зондирование искривления пространства-времени

Фотосфера — это область вокруг черной дыры, где фотоны могут вращаться по неустойчивым орбитам. Радиус фотосферы напрямую определяет размер тени черной дыры, а её форма — её очертания. Фотоны, проходящие достаточно близко к черной дыре, но не попадающие в неё, будут отклоняться гравитацией, создавая видимую тень. Из-за неустойчивости орбит фотоны, находящиеся в фотосфере, либо спирально приближаются к черной дыре, либо удаляются от неё, что приводит к формированию чётко очерченной тени, размер и форма которой зависят от массы и спина черной дыры, а также от параметров, описывающих отклонения от метрики Шварцшильда. Таким образом, анализ формы и размера тени черной дыры позволяет косвенно изучать геометрию пространства-времени вблизи горизонта событий.

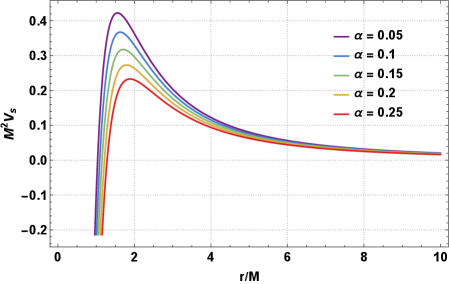
Расчет траекторий фотонов вблизи зарятой чёрной дыры Хейварда требует анализа её эффективного потенциала. Этот потенциал, зависящий от метрики пространства-времени, определяет условия движения фотонов и возможность существования устойчивых или неустойчивых орбит. Форма эффективного потенциала V_{eff}(r, \theta) позволяет определить критические значения энергии и углового момента, при которых фотоны могут захватываться гравитацией чёрной дыры или отклоняться от неё. Именно анализ этого потенциала позволяет вычислять радиус фотонной сферы и, как следствие, размер тени чёрной дыры, предоставляя возможность проверки предсказаний общей теории относительности.

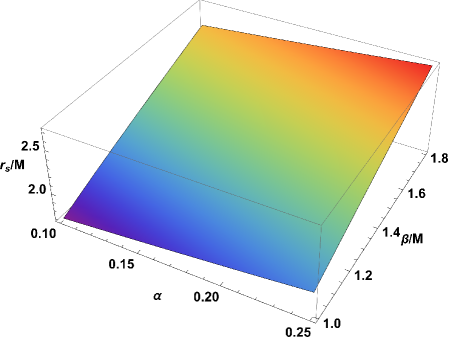
Как показано в Таблицах 2-3, параметры α и β оказывают существенное влияние на радиус фотонной сферы (r_s/M). Анализ демонстрирует, что увеличение значений α и β приводит к пропорциональному увеличению радиуса фотонной сферы. В частности, установлено, что для различных комбинаций α и β, радиус фотонной сферы может изменяться в пределах, значимых для наблюдаемых характеристик тени черной дыры. Количественные данные, представленные в таблицах, позволяют оценить степень влияния каждого параметра на геометрию фотонной сферы и, следовательно, на размер и форму тени черной дыры.

Результаты, представленные на рисунках 5, демонстрируют, что параметры α и β оказывают прямое влияние на радиус тени черной дыры. Увеличение значений α и β приводит к пропорциональному увеличению радиуса тени, что является измеримым эффектом, проявляющимся в наблюдаемой силуэте черной дыры. Данное увеличение радиуса тени позволяет проводить количественную оценку параметров α и β, тем самым предоставляя возможность для проверки и уточнения моделей черных дыр и общей теории относительности на основе астрономических наблюдений. Изменение радиуса тени, вызванное изменением α и β, является наблюдаемым проявлением геометрии пространства-времени вблизи черной дыры.

Тень черной дыры, возникающая как результат гравитационного искривления света, служит прямым зондом геометрии пространства-времени вблизи горизонта событий. Анализ формы и размера этой тени позволяет проверить предсказания общей теории относительности, в частности, отклонения от ньютоновской гравитации в сильных гравитационных полях. Измерения радиуса тени и асимметрии ее формы предоставляют данные для оценки параметров черной дыры, таких как масса и спин, а также для поиска отклонений от метрики Керра, что может указывать на наличие экзотической материи или модификаций теории гравитации. Таким образом, наблюдение и анализ тени черной дыры представляют собой важный инструмент для тестирования фундаментальных принципов физики.

Внутренние орбиты и прецессия: динамика вблизи чёрной дыры

Внутренняя стабильная круговая орбита (ВСКО) определяет внутреннюю границу стабильного существования аккреционного диска вокруг чёрной дыры. Орбиты, находящиеся ближе ВСКО, нестабильны, и материя, находящаяся на них, неизбежно спирально упадёт на чёрную дыру. Радиус ВСКО зависит от спина чёрной дыры, описываемого параметром a, и её массы M. Для невращающейся чёрной дыры ( a = 0 ) радиус ВСКО равен 6 GM/c^2, где G — гравитационная постоянная, а c — скорость света. С увеличением спина чёрной дыры радиус ВСКО уменьшается, что позволяет аккреционному диску приближаться ближе к горизонту событий и увеличивать эффективность аккреции.

Вычисление радиуса внутренней стабильной круговой орбиты (ISCO) и частоты прецессии периастра требует знания эффективного потенциала и геометрии пространства-времени вокруг черной дыры. Эффективный потенциал, учитывающий как гравитационное притяжение, так и вращательное воздействие черной дыры, определяет допустимые орбиты аккреционного диска. Радиус ISCO рассчитывается как минимальное значение радиуса, при котором круговая орбита остается стабильной. Частота прецессии периастра, описывающая поворот эллиптической орбиты в плоскости, зависит от метрики пространства-времени, в частности, от параметров вращения черной дыры и массы M. Поскольку геометрия пространства-времени вокруг вращающейся черной дыры описывается метрикой Керра, вычисление ISCO и частоты прецессии требует решения уравнений геодезических в этом искривленном пространстве-времени.

Как было показано в проведенных расчетах, увеличение соотношения \beta/M и α приводит к увеличению частоты прецессии периастра. При этом наблюдается подавление вертикальной частоты. Данная зависимость обусловлена изменением эффективного потенциала и, как следствие, модификацией траектории движения объекта в искривленном пространстве-времени вокруг черной дыры. Более высокие значения параметров β и α усиливают релятивистские эффекты, что приводит к более быстрому изменению ориентации орбиты и, соответственно, к увеличению частоты прецессии периастра, одновременно уменьшая частоту вертикальных колебаний.

Характеристики орбит, такие как положение и частота прецессии периастра, предоставляют важные данные для понимания процессов аккреции на черные дыры. Изменения в параметрах \beta/M и α, влияющие на частоту прецессии, позволяют оценить скорость и эффективность аккреции вещества. Анализ этих характеристик также дает информацию о механизмах извлечения энергии из черной дыры, в частности, об эффективности процессов, связанных с вращением черной дыры и магнитными полями, которые определяют структуру аккреционного диска и его взаимодействие с черной дырой.

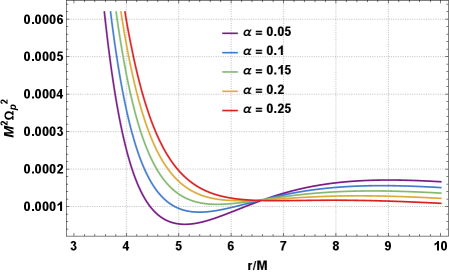
Квазинормальные моды: отклик чёрной дыры на возмущения

Скалярные возмущения, представляющие собой отклонения в геометрии пространства-времени, описываемые скалярными полями, позволяют исследовать динамический отклик чёрной дыры на внешние воздействия. Эти возмущения возникают как решения волнового уравнения, в частности, уравнения Клейна-Гордона, применительно к метрике чёрной дыры. Анализ этих возмущений показывает, что чёрная дыра не является абсолютно статичным объектом, а способна к колебаниям и излучению, характеризующемуся специфическим спектром частот. Изучение этих колебаний позволяет получить информацию о массе, спину и других параметрах чёрной дыры, а также о свойствах пространства-времени вблизи неё. \delta g_{\mu\nu} представляет собой тензор возмущений, описывающий отклонение метрики от метрики Шварцшильда.

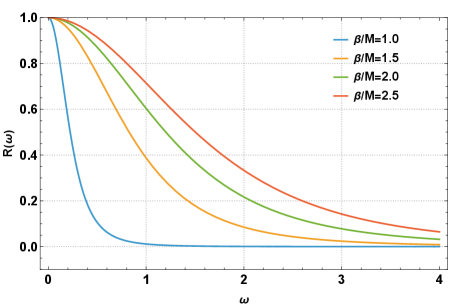
Для анализа скалярных возмущений, возникающих в пространстве-времени вокруг черной дыры, используется уравнение Клейна-Гордона. Решение этого уравнения в общем случае затруднительно, поэтому применяется приближение ВКБ (Вентцеля-Крамерса-Бриллюэна). В рамках этого приближения, решение ищется в виде \psi(t,r) \approx A(r) e^{-i\omega t} , где ω является комплексной частотой. Реальная часть ω определяет частоту колебаний, а мнимая часть — скорость затухания. Полученные комплексные частоты ω и соответствующие им моды колебаний называются квазинормальными модами, и они характеризуют специфический отклик черной дыры на внешние возмущения, определяя характер затухающих колебаний, наблюдаемых в различных сигналах.

Наблюдаемые квазипериодические осцилляции в рентгеновском излучении аккрецирующих чёрных дыр напрямую связаны с квазинормальными модами. Эти моды возникают как собственные частоты возмущений гравитационного поля чёрной дыры и проявляются в характерных частотах и времени затухания осцилляций. Анализ спектральных характеристик этих осцилляций позволяет оценить массу и спин чёрной дыры, а также проверить предсказания общей теории относительности. Частоты квазинормальных мод зависят от параметров чёрной дыры и типа возмущения, что делает их мощным инструментом для изучения свойств этих объектов. \omega = \frac{1}{2\pi R} \sqrt{ \frac{n^2}{R^2} + a^2} где ω — частота моды, R — радиус горизонта событий, а a — параметр спина.

За горизонтом стандартной модели: тёмная материя и струнные облака

Заряженная метрика Хейварда, представляющая собой расширение классической общей теории относительности, предоставляет уникальную возможность включения в модель чёрной дыры дополнительных физических эффектов, таких как совершенная жидкость тёмной материи. В отличие от стандартных решений, которые рассматривают чёрную дыру в вакууме, данная модель допускает наличие окружения из тёмной материи, влияющего на геометрию пространства-времени вокруг объекта. Это достигается путем включения в уравнения Эйнштейна тензора энергии-импульса, описывающего свойства совершенной жидкости, что позволяет исследовать, каким образом тёмная материя модифицирует структуру чёрной дыры и её наблюдаемые характеристики. R_{\mu\nu} - \frac{1}{2}Rg_{\mu\nu} = 8\pi T_{\mu\nu}, где T_{\mu\nu} представляет собой тензор энергии-импульса совершенной жидкости. Такой подход позволяет не только изучать взаимодействие чёрных дыр с тёмной материей, но и проверять альтернативные теории гравитации, предсказывающие существование экзотических форм материи.

Включение параметров струнных облаков существенно модифицирует геометрию пространства-времени вокруг чёрных дыр. Исследования показывают, что эти облака, состоящие из одномерных топологических дефектов, влияют на метрику Шварцшильда, изменяя кривизну пространства. Данное изменение, в свою очередь, оказывает заметное влияние на наблюдаемые астрономические характеристики, в частности, на форму и размер тени чёрной дыры. Тень чёрной дыры, являясь одним из наиболее прямых способов визуализации этих объектов, становится чувствительным инструментом для проверки предсказаний, сделанных на основе моделей, включающих струнные облака. Анализ формы и размера этой тени позволяет оценить параметры струнных облаков и, таким образом, проверить возможность существования экзотических состояний материи и альтернативных теорий гравитации, выходящих за рамки общей теории относительности. R_{\mu\nu} = 0 — классическое уравнение Эйнштейна, которое модифицируется при учете влияния струнных облаков.

Предложенные модификации геометрии пространства-времени вокруг чёрных дыр открывают уникальную возможность для проверки альтернативных теорий гравитации, выходящих за рамки общей теории относительности Эйнштейна. Включение параметров струнных облаков и эффектов, связанных с экзотической материей, такой как тёмная материя, позволяет исследовать взаимодействие чёрных дыр с этими загадочными компонентами Вселенной. Анализ наблюдаемых характеристик, например, тени чёрной дыры, становится инструментом для сопоставления теоретических моделей с астрономическими данными, что потенциально может указать на отклонения от предсказаний стандартной гравитации и пролить свет на природу тёмной материи и её роль в формировании структуры космоса. Такой подход не только углубляет понимание гравитационных явлений, но и способствует развитию новых физических теорий, способных объяснить наиболее сложные и необъяснимые аспекты Вселенной.

Исследование, представленное в данной работе, углубляется в сложные взаимодействия между чёрными дырами, тёмной материей и струнными облаками. Анализ геодезических и квазинормальных мод, проводимый авторами, демонстрирует, что даже малейшие отклонения от стандартных моделей могут нести в себе богатую информацию о фундаментальных свойствах пространства-времени. В этом контексте, как заметил Иммануил Кант: “Действуй так, чтобы максима твоя могла стать всеобщим законом”. Подобно тому, как каждый алгоритм кодирует мировоззрение, любая модель чёрной дыры — это моральный акт, отражающий наши представления о Вселенной и, следовательно, требующий строгой проверки и этической ответственности в интерпретации полученных результатов. Понимание влияния тёмной материи и струнных облаков на характеристики чёрной дыры — это не просто научный поиск, но и попытка создать более полную и адекватную картину мира.

Куда двигаться дальше?

Представленная работа, углубляясь в тонкости зарятой чёрной дыры Хейварда в окружении тёмной материи и струнных облаков, неизбежно ставит вопрос о границах применимости существующих моделей. Изучение геодезических и квазинормальных мод — ценный инструмент, но он остаётся лишь приближением к сложной реальности. Необходимо признать, что математическая элегантность не гарантирует физической достоверности, и что каждая упрощающая гипотеза несёт в себе потенциальную погрешность.

Будущие исследования должны сосредоточиться не только на уточнении параметров, но и на развитии новых, более комплексных моделей, учитывающих нелинейные эффекты и взаимодействие различных физических полей. Особое внимание следует уделить проблеме наблюдательной верификации: как можно отличить предсказанные теорией отклонения от случайных флуктуаций? Инженер несёт ответственность не только за работоспособность системы, но и за её последствия, и это особенно актуально при моделировании столь экзотических объектов, как чёрные дыры.

Прогресс без этики — это ускорение без направления. Каждый алгоритм кодирует мировоззрение, и необходимо помнить, что наша задача — не просто описывать Вселенную, но и понимать её, а значит, учитывать все возможные последствия наших открытий. Этика должна масштабироваться вместе с технологией, и только тогда мы сможем двигаться вперёд, не теряя из виду главную цель — познание истины.

---

Оригинал статьи: https://arxiv.org/pdf/2602.02621.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.

• Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip

• Все рецепты культистского круга в Escape from Tarkov

• Нечестивцам нет покоя: как получить старый ключ от коттеджа

• Решение головоломки с паролем Absolum в Yeldrim.

• Arknights: Endfield — Интерактивная карта (Долина IV)

• Акции UGLD. Южуралзолото ГК: прогноз акций.

• Лучшие шаблоны дивизий в Hearts Of Iron 4

• Келли Эллард сейчас: где сегодня убийца под мостом?

• Прогнозы криптовалюты AXS: информация о ценах на AXS

2026-02-04 20:56