Тензорные сети в релятивистской квантовой теории поля: новый подход к непертурбативным расчетам

Автор: Денис Аветисян

В данной статье представлен алгоритм римановой оптимизации для решения проблемы регуляризации в многопольных релятивистских непрерывных тензорных сетях (RCMPS).

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Многообразие RCMPS, параметризованное матрицами $R\_1$, $R\_2$ и $Q$, представлено как подпространство полного гильбертова пространства $\mathscr{H}$ теории поля, при этом область допустимых значений, где матрицы $R\_1$ и $R\_2$ коммутируют, образует подмногообразие $\mathcal{M}\_{\text{reg}}$.

Исследование непертурбативных эффектов и фазовых переходов, таких как переход Беркса-Кирпатрика, с использованием оптимизированных многопольных RCMPS.

Несмотря на перспективность тензорных сетей как вариационного метода для изучения квантовых теорий поля, применение релятивистских непрерывных матричных произведений состояний (RCMPS) к моделям с несколькими полями сталкивалось с проблемой расходимости, требующей выполнения специфических условий регуляризации. В настоящей работе, посвященной ‘Multi-Field Relativistic Continuous Matrix Product States’, предложен алгоритм римановой оптимизации, позволяющий минимизировать энергию плотности на регуляризированном подмногообразии RCMPS и получать чисто вариационные результаты. Демонстрируется эффективность метода на примере двух взаимодействующих скалярных полей в $(1+1)$ измерениях, позволяя исследовать фазы спонтанного нарушения симметрии и переход Березинского-Костерлица-Таулеса. Открывает ли это путь к более точному исследованию непертурбативных аспектов квантовых теорий поля с помощью RCMPS?

За гранью возмущений: Необходимость непертурбативных методов

Традиционная квантовая теория поля широко использует теорию возмущений для приближенного решения сложных задач. Однако, данный подход сталкивается с серьезными трудностями при исследовании систем с сильными корреляциями, где взаимодействие между частицами настолько велико, что стандартные методы перестают работать эффективно. В таких системах, как высокотемпературная сверхпроводимость или конфайнмент в квантовой хромодинамике, возмущения не могут быть рассмотрены как малые добавки к основному состоянию, что делает теорию возмущений неприменимой и требующей разработки альтернативных, непертурбативных методов для получения точных и надежных результатов. Данное ограничение существенно затрудняет понимание физических свойств и поведения этих сложных квантовых систем.

Ограничения, с которыми сталкивается теория возмущений, особенно остро проявляются при изучении таких явлений, как высокотемпературная сверхпроводимость и конфайнмент в квантовой хромодинамике. В высокотемпературных сверхпроводниках сильное взаимодействие между электронами приводит к отклонению от стандартных моделей, основанных на слабом взаимодействии, что делает приближения теории возмущений неадекватными. Аналогично, в квантовой хромодинамике, описывающей сильные взаимодействия кварков и глюонов, конфайнмент — явление, когда кварки никогда не наблюдаются в свободном состоянии — требует методов, способных учитывать непертурбативные эффекты. Попытки описать эти явления в рамках стандартной теории возмущений приводят к расходящимся результатам и не позволяют получить физически осмысленные предсказания, подчеркивая необходимость разработки альтернативных, непертурбативных подходов для полноценного понимания этих сложных квантовых систем.

Для адекватного описания сложных квантовых систем, характеризующихся сильными корреляциями между частицами, необходим мощный непертурбативный подход, выходящий за рамки приближений. Традиционные методы, основанные на теории возмущений, зачастую оказываются неэффективными при рассмотрении систем, где взаимодействие между компонентами сопоставимо с энергией самих частиц. В таких случаях приближения теряют точность, и требуется разработка альтернативных подходов, способных учитывать все возможные взаимодействия без упрощений. Такие методы, как метод функциональной интеграции и решетчатая квантовая хромодинамика, стремятся к этому, позволяя исследовать системы, где стандартные вычисления оказываются невозможными, и пролить свет на явления, такие как высокотемпературная сверхпроводимость и конфайнмент в квантовой хромодинамике. Их применение открывает перспективы для более глубокого понимания фундаментальных свойств материи и разработки новых материалов с уникальными характеристиками.

Современные вычислительные методы в квантовой теории поля сталкиваются с фундаментальным ограничением: неспособностью эффективно исследовать полное гильбертово пространство взаимодействующих квантовых полей. Это пространство, описывающее все возможные состояния системы, экспоненциально растёт с увеличением числа частиц и сложности взаимодействий. Традиционные подходы, даже с использованием самых мощных суперкомпьютеров, способны охватить лишь незначительную его часть, что приводит к неполному и зачастую неточному описанию явлений, особенно в системах с сильным взаимодействием. Невозможность адекватно учесть все возможные квантовые состояния препятствует пониманию таких загадочных явлений, как высокотемпературная сверхпроводимость и конфайнмент в квантовой хромодинамике, требуя разработки принципиально новых, непертурбативных методов, способных преодолеть это вычислительное ограничение и исследовать всю сложность квантового мира.

Результаты RCMPS демонстрируют отличное соответствие теории возмущений при слабом взаимодействии и превосходят её по точности при умеренных значениях параметра взаимодействия g ≥ 0.3, даже при минимальной глубине потенциала.

Тензорные сети: Новый язык квантовых состояний

Сетевые тензоры представляют собой мощный вариационный подход (анзац) для описания многочастичных квантовых состояний, обеспечивающий компактное и эффективное представление. В отличие от традиционных методов, требующих экспоненциального роста вычислительных ресурсов с увеличением числа частиц, сетевые тензоры используют структуру запутанности для уменьшения необходимого объема памяти и вычислительной сложности. Это достигается за счет представления волновой функции в виде сети тензоров, где каждый тензор связан с определенной подсистемой. Размерность тензоров ограничивается, что позволяет эффективно моделировать системы с большим числом частиц, сохраняя при этом достаточную точность для описания физических свойств. Например, в системах с одномерной структурой, таких как цепочки спинов, матричные произведения состояний (MPS) являются эффективным представлением, требующим лишь полиномиального роста ресурсов с увеличением числа частиц. Таким образом, сетевые тензоры обеспечивают практичный инструмент для изучения сложных квантовых систем, недоступных для точного решения традиционными методами.

Традиционные методы описания многочастичных квантовых состояний сталкиваются с экспоненциальным ростом размерности гильбертова пространства по мере увеличения числа частиц, что делает точные вычисления практически невозможными даже для умеренных систем. Тензорные сети, напротив, используют структуру запутанности между частицами для эффективного представления этих состояний. Вместо хранения полного вектора состояния в гильбертовом пространстве размерности $2^N$ (где N — число частиц), тензорные сети оперируют с тензорами меньшего размера, соединенными между собой. Эта структура позволяет представить квантовое состояние, сохраняя информацию о наиболее значимых корреляциях между частицами, и существенно сократить вычислительные затраты, приближаясь к полиномиальной сложности в зависимости от числа частиц.

Непрерывные матричные произведения состояний (CMPS) представляют собой расширение метода матричных произведений состояний (MPS) для применения к нерелятивистским квантовым теориям поля. В отличие от дискретных систем, где MPS оперируют с конечным набором состояний, CMPS используют непрерывные переменные для описания степеней свободы поля. Это позволяет эффективно аппроксимировать волновые функции, описывающие частицы в квантовом поле, используя ограниченное число параметров, что существенно снижает вычислительную сложность. Формально, CMPS определяются как тензорные сети, где индексы, соответствующие непрерывным координатам пространства, интегрируются по непрерывной области. Такой подход позволяет представлять многочастичные состояния с высокой точностью, обходя проблему экспоненциального роста размерности гильбертова пространства, характерную для традиционных методов квантовой теории поля.

Релятивистские непрерывные тензорные сети (РНТС) представляют собой перспективный подход к моделированию релятивистских квантовых теорий поля, сохраняя вычислительную эффективность, характерную для нерелятивистских аналогов, таких как непрерывные произведения состояний (НПС). В отличие от традиционных методов, которые сталкиваются с экспоненциальным ростом вычислительных затрат при описании многочастичных систем, РНТС используют структуру запутанности для эффективного представления волновых функций. Ключевым аспектом является использование непрерывных переменных для описания степеней свободы поля, что позволяет избежать дискретизации пространства и времени, часто возникающей в численных расчетах. Это особенно важно для релятивистских теорий, где динамика зависит от непрерывных координат и требует точного описания поведения поля на различных масштабах. Таким образом, РНТС предлагают масштабируемый метод для исследования физики высоких энергий и космологии.

Зависимость энтропии спутанности RCMPS от параметра g при различных размерах связи D демонстрирует влияние g на степень запутанности системы.

RCMPS: Реализация и ключевые ограничения

Метод RCMPS (Renormalized Coupling Map Perturbation Scheme) основывается на формализме функционального интеграла для определения квантовой теории поля. В рамках этого подхода, физические величины вычисляются как функциональные интегралы от полей, а для обеспечения сходимости и получения физически осмысленных результатов применяется процедура нормального упорядочения операторов. Нормальное упорядочение предполагает перестановку операторов рождения и уничтожения таким образом, чтобы операторы уничтожения предшествовали операторам рождения, что позволяет исключить расходимости, возникающие при вычислении вакуумных флуктуаций и вкладов петель. В частности, функциональный интеграл представляется в виде $Z = \int D\phi \, e^{iS[\phi]}$, где $S[\phi]$ — действие, а процедура нормального упорядочения применяется к операторам в этом действии для получения конечных результатов.

Ключевым аспектом метода RCMPS является обеспечение регулярности тензорной сети, которое обеспечивается посредством выполнения условия регулярности [$R_j, R_k = 0$]. Данное условие необходимо для получения конечной плотности энергии и корректно сформулированной вариационной задачи для многокомпонентного RCMPS. Нарушение условия регулярности приводит к расходимостям в вычислениях и невозможности получения физически осмысленных решений. Таким образом, поддержание [$R_j, R_k = 0$] является обязательным требованием для стабильности и корректности численной реализации метода RCMPS.

Метод Римановой оптимизации применяется для итеративной минимизации плотности энергии в пространстве регулярных конфигураций RCMPS. Этот процесс включает в себя определение функционала энергии, зависящего от параметров конфигурации, и последующее использование алгоритмов оптимизации на римановом многообразии, образованном этими параметрами. Итерации включают вычисление градиента функционала энергии и обновление параметров конфигурации в направлении, противоположном градиенту, с целью достижения локального минимума. Выбор подходящей метрики на римановом многообразии играет ключевую роль в эффективности и скорости сходимости алгоритма, обеспечивая стабильное и точное минимизирование $E = \int d^3x \mathcal{H}(x)$.

Представление в виде матрицы переноса (Transfer Matrix) обеспечивает эффективный анализ динамики и свойств системы RCMPS. Данный метод позволяет свести многомерную задачу к одномерной, представляя эволюцию системы как последовательное применение матрицы переноса к начальному состоянию. Это упрощает вычисление корреляционных функций, энергии основного состояния и других физических величин. Матрица переноса, построенная на основе тензорной сети RCMPS, содержит информацию о локальных взаимодействиях и позволяет исследовать критическое поведение системы, а также рассчитывать различные наблюдаемые величины, такие как $E = Tr(T)$ где $T$ — матрица переноса.

Наблюдаемые параметры порядка чётко демонстрируют различные сценарии нарушения симметрии в процессе фазового перехода при D=18 как для g>λ, так и для λ>g.

Проявляющаяся физика и мощь RCMPS

Метод Решетчатых Тензорных Сетей для Релятивистских Квантовых Полей (RCMPS) значительно расширяет возможности применения тензорных сетевых методов к изучению релятивистской квантовой механики, включая описание таких сложных систем, как поле Дирака. Традиционные подходы часто сталкиваются с трудностями при моделировании релятивистских эффектов, однако RCMPS позволяет эффективно представлять и исследовать квантовые поля в пространстве-времени, используя дискретизацию и оптимизацию тензорных сетей. Это открывает новые перспективы для анализа динамических свойств частиц, взаимодействия и фазовых переходов в релятивистских системах, а также для изучения непертурбативных эффектов, которые недоступны для стандартных методов теории поля. По сути, RCMPS предоставляет мощный инструмент для приближенного решения сложных релятивистских квантовых задач, преодолевая ограничения традиционных вычислительных подходов.

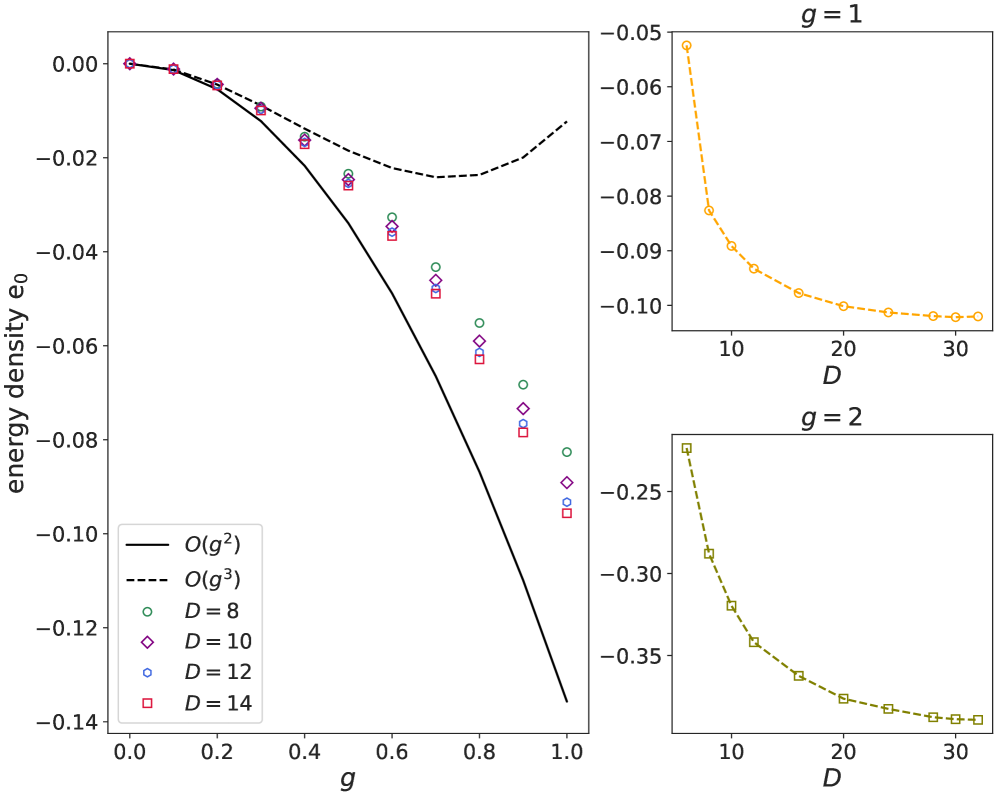
Метод RCMPS предоставляет уникальную возможность исследовать топологические фазовые переходы, такие как переход Березинского-Костерлица-Таулеса (BKT), в рамках релятивистской квантовой теории поля. В отличие от традиционных подходов, часто ограниченных нерелятивистскими системами, RCMPS позволяет изучать критическое поведение в сценариях, где эффекты специальной теории относительности играют существенную роль. Наблюдение пика в энтропии запутанности, полученное с помощью RCMPS, указывает на возможность протекания BKT-перехода, характеризующегося появлением топологического порядка и разрывом в энергии возбуждений, даже при увеличении размерности связи. Это открывает новые перспективы для понимания квантовых систем с экзотическими фазами и топологическими свойствами, ранее недоступными для исследования с помощью стандартных методов.

Анализ энтропии запутанности предоставляет мощный инструмент для характеристики квантовых корреляций, присутствующих в основном состоянии сложной квантовой системы. Этот показатель, измеряющий степень взаимосвязанности между различными частями системы, позволяет выявить нетривиальные топологические фазы и определить наличие или отсутствие дальних квантовых корреляций. В рамках исследования, вычисление энтропии запутанности позволило обнаружить пик, указывающий на возможность Березинского-Костерлица-Таулеса (BKT) перехода, что свидетельствует о возникновении новых фаз материи, характеризующихся нелокальными квантовыми эффектами. Устойчивость разрыва в энтропии при увеличении размерности связи подтверждает наличие сильных корреляций и нетривиальную структуру основного состояния, что делает этот метод ключевым для изучения сложных квантовых систем и их топологических свойств.

Метод RCMPS, использующий симметрию $D_4$, предоставляет уникальную возможность изучения сложных систем, превосходящую возможности стандартных методов теории возмущений. Проверка показала соответствие результатов, полученных с помощью RCMPS, с предсказаниями теории возмущений в области слабых взаимодействий. Однако, при моделировании $D_4$-симметричного скалярного поля наблюдались отчетливые паттерны спонтанного нарушения симметрии, недоступные для анализа с использованием традиционных подходов. Ключевым результатом стало обнаружение пика в энтропии запутанности, что указывает на возможность протекания перехода Березинского-Костерлица-Таулеса (BKT). Примечательно, что с увеличением размерности связи сохраняется разрыв в энтропии, подтверждающий нетривиальный характер этого фазового перехода и потенциальную возможность изучения новых состояний материи.

Представленная работа демонстрирует стремление к преодолению границ применимости существующих физических законов, что находит отклик в известном высказывании Альберта Эйнштейна: «Самое прекрасное, что мы можем испытать, — это тайна. Источник всего истинного искусства и науки». Исследование регуляризации в многопольных релятивистских непрерывных тензорных сетях (RCMPS) является попыткой проникнуть в эту тайну, исследуя непертурбативные режимы квантовой теории поля. Подобно тому, как чёрная дыра испытывает границы нашего понимания, так и RCMPS подталкивает исследователей к переосмыслению существующих методов и поиску новых подходов к описанию сложных физических явлений, таких как BKT-переходы. Когнитивное смирение исследователя пропорционально сложности нелинейных уравнений Эйнштейна, и данная работа служит ярким тому подтверждением.

Что же дальше?

Представленный подход, манипулируя с непрерывными тензорными сетями в релятивистской области, несомненно, расширяет инструментарий для изучения непертурбативных квантовых теорий поля. Однако, за кажущейся точностью скрывается та же старая проблема: любая модель, даже самая изящная, есть лишь эхо наблюдаемого. Регуляризационные условия, пусть и смягченные римановым алгоритмом, остаются искусственным ограничением, наложенным на природу, которая, возможно, принципиально нерегулярна.

Поиск комплексных фаз, таких как переходы БКТ, не является самоцелью. Важнее признать, что сингулярности, будь то в теории поля или в геометрии пространства-времени, представляют собой границы нашего понимания. Если кажется, что сингулярность понята, это иллюзия, тень, отбрасываемая ограниченностью используемых методов. Дальнейшие исследования, вероятно, потребуют радикального пересмотра фундаментальных предпосылок, отказа от привычных представлений о непрерывности и локальности.

Истинно фундаментальный прорыв, возможно, потребует не улучшения существующих инструментов, а создания принципиально новых, способных заглянуть за горизонт событий, где привычные законы перестают действовать. Это не вопрос вычислительной мощности или математической изобретательности, а вопрос смирения перед лицом непознаваемого.

Оригинал статьи: https://arxiv.org/pdf/2511.20762.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-29 07:39