Топологические дефекты фазовых диаграмм: в поисках особых точек

Автор: Денис Аветисян

Новое исследование предлагает теоретическую основу для понимания сингулярностей, возникающих в фазовых переходах многочастичных систем, и их связи с возникающими симметриями.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал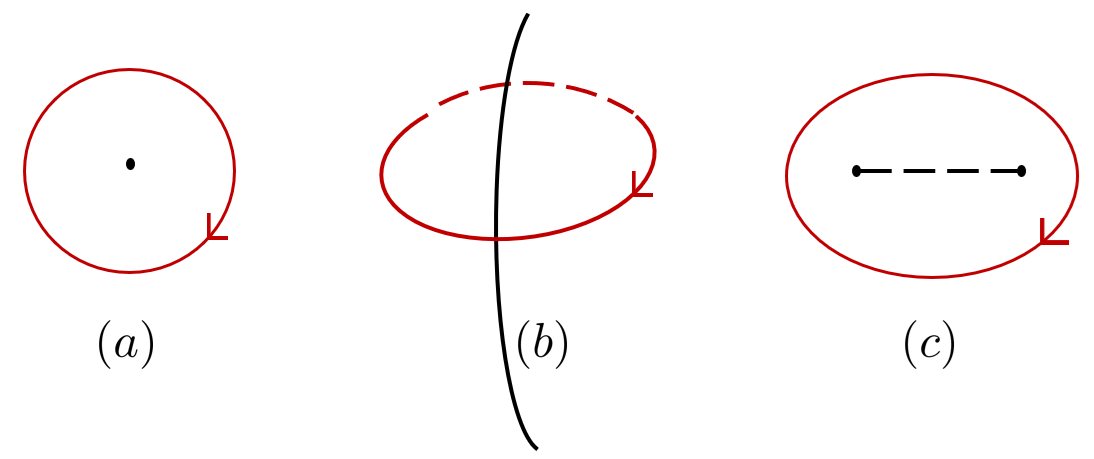

Диавольская критическая точка возникает в параметрическом пространстве, когда семейство решений, лежащее на сфере <span class="katex-eq" data-katex-display="false">S^{N-1}</span>, приводит к сингулярности коразмерности <span class="katex-eq" data-katex-display="false">N</span>, причём добавление дополнительных параметров в <span class="katex-eq" data-katex-display="false">\mathbb{R}^{n}</span>, где <span class="katex-eq" data-katex-display="false">n > N</span>, не отменяет существование такой точки, если коразмерность сингулярной поверхности остаётся равной <span class="katex-eq" data-katex-display="false">N</span>, однако уменьшение коразмерности сингулярной поверхности ниже <span class="katex-eq" data-katex-display="false">N</span> исключает возможность возникновения диавольской критической точки. — Диавольская критическая точка возникает в параметрическом пространстве, когда семейство решений, лежащее на сфере $S^{N-1}$ , приводит к сингулярности коразмерности $N$ , причём добавление дополнительных параметров в $\mathbb{R}^{n}$ , где $n > N$ , не отменяет существование такой точки, если коразмерность сингулярной поверхности остаётся равной $N$ , однако уменьшение коразмерности сингулярной поверхности ниже $N$ исключает возможность возникновения диавольской критической точки.

В работе рассматриваются ‘дьявольские критические точки’ и их роль в описании топологических дефектов на фазовых диаграммах.

Фазовые переходы, традиционно рассматриваемые как точки бифуркации в пространстве параметров систем, могут быть обобщены на более сложные топологические дефекты. В работе ‘In search of diabolical critical points’ исследуются такие дефекты высшей кодименсионности, характеризующиеся нетривиальным закручиванием равновесных состояний вокруг сингулярности. Предлагается понятие «дьявольской критической точки» (DCP), аналогичной непрерывному фазовому переходу, но с заменой фаз материи на нетривиальное закручивание состояний. Каковы общие принципы, определяющие стабильность DCP и их проявление в различных квантовых и классических многочастичных системах?

За гранью привычных фаз: Зов топологической организации

Традиционные фазовые диаграммы, основанные на параметрах упорядочения, зачастую оказываются недостаточными для описания сложных состояний материи, возникающих из-за топологических дефектов. Эти дефекты, такие как вихри или дислокации, представляют собой нарушения в структуре материала, которые не могут быть охарактеризованы простыми параметрами порядка. В результате, системы с богатой топологией могут демонстрировать фазы и переходы, не предсказуемые стандартными методами. Например, в сверхпроводниках вихри магнитного поля могут формировать сложные структуры, влияющие на их электрические свойства, а в жидкокристаллических материалах дефекты могут приводить к появлению новых оптических характеристик. Понимание роли топологических дефектов необходимо для полного описания поведения конденсированных сред и разработки новых материалов с уникальными свойствами.

Понимание дефектов, таких как вихри, играет ключевую роль в описании систем, демонстрирующих нетрадиционные фазы и фазовые переходы. Эти дефекты — это не просто незначительные отклонения от идеальной структуры, а фундаментальные элементы, определяющие макроскопические свойства вещества. В системах, где обычные параметры порядка не способны адекватно описать поведение, именно топологические дефекты формируют новые фазы, определяя их стабильность и характеристики. Например, в сверхпроводниках вихри магнитного поля проникают в материал, формируя смешанное состояние, отличающееся от полностью сверхпроводящего или нормального. Аналогичные явления наблюдаются в жидких кристаллах и других материалах, где дефекты влияют на оптические, электрические и механические свойства. Изучение топологии этих дефектов позволяет не только объяснить наблюдаемые феномены, но и предсказывать появление новых, ранее неизвестных фаз материи, открывая возможности для создания материалов с уникальными характеристиками.

Классические системы, несмотря на кажущуюся простоту и полноту их описания в рамках традиционных моделей, способны демонстрировать неожиданно сложное поведение при наличии топологических особенностей. Исследования показывают, что даже в хорошо изученных физических системах, таких как сверхпроводники или жидкие кристаллы, появление топологических дефектов — вихрей, дислокаций, доменных границ — кардинально меняет их свойства. Эти дефекты, обладая нетривиальной топологией, определяют новые фазы материи и типы переходов между ними, которые не могут быть предсказаны стандартными подходами, основанными на анализе порядка. Более того, взаимодействие этих дефектов друг с другом и с окружающей средой приводит к возникновению коллективных явлений, требующих применения новых теоретических инструментов и экспериментальных методов для их понимания и описания.

Топология как архитектор фазовых переходов

Переход Костерлица-Таулеса является примером фазового перехода, обусловленного исключительно развязкой топологических дефектов. В отличие от традиционных фазовых переходов, характеризующихся изменением параметра порядка, данный переход происходит без изменения глобального упорядочения системы. Суть перехода заключается в изменении топологии дефектов: при понижении температуры происходит связывание пар дефектов, уменьшая их плотность и увеличивая эффективный радиус корреляции. Критическая точка перехода определяется моментом, когда энергия, необходимая для создания отдельных дефектов, становится меньше энергии, связанной с их связыванием, что приводит к экспоненциальному увеличению плотности несвязанных дефектов и качественному изменению свойств системы. Этот процесс демонстрирует, что топологические характеристики дефектов могут определять фазовое поведение материала, даже при отсутствии классического параметра порядка.

В отличие от традиционных фазовых переходов, характеризующихся изменением порядка, некоторые фазовые переходы, такие как переход Костерлица-Таулеса, происходят без изменения макроскопического параметра порядка. Вместо этого, определяющим фактором является качественное изменение плотности и поведения топологических дефектов в системе. Увеличение плотности дефектов, изменение их мобильности или конфигурации приводят к фундаментальным изменениям в физических свойствах материала, таких как проводимость или магнитные характеристики, без необходимости изменения какого-либо глобального параметра порядка. Данный механизм фазового перехода подчеркивает важную роль топологических дефектов как носителей информации о фазе системы.

Наличие фазовой границы, разделяющей различные фазы материи, тесно связано с поведением топологических дефектов и их влиянием на свойства системы. Изменение плотности и характера этих дефектов, таких как вихри или дислокации, приводит к качественным изменениям в макроскопических характеристиках материала. В частности, фазовый переход может происходить не из-за изменения порядка параметра, а из-за изменения топологии дефектов — их количества, расположения и взаимодействия. Переход через фазовую границу характеризуется резким изменением свойств, определяемых коллективным поведением этих дефектов, и может приводить к появлению новых состояний материи с уникальными характеристиками. $\Delta G = \Delta H - T\Delta S$

Математический арсенал: Описывая топологический порядок

Волокнистые расслоения представляют собой математический аппарат, позволяющий описывать пространства, параметризованные топологическими свойствами. В рамках данной концепции, пространство рассматривается как объединение копий некоторого многообразия (волокна), параметризованных базовым пространством. Это позволяет систематизировать описание степеней свободы системы, поскольку топологические свойства базового пространства определяют ограничения на конфигурации волокон. Формально, волокнистое расслоение определяется тройкой (E, B, π), где E — полное пространство, B — базовое пространство, а π — проекция, отображающая точки из E в B. Такое представление обеспечивает удобный инструмент для анализа систем, в которых важны глобальные топологические характеристики, а не только локальные свойства.

Топологические дефекты в материалах описываются с использованием пространств, определяемых такими геометрическими объектами, как окружности ( $S^1$ ), сферы ( $S^2$ ) и трехмерные сферы ( $S^3$ ). Эти объекты не рассматриваются как геометрические фигуры в обычном смысле, а как топологические пространства, определяющие возможные конфигурации дефектов. Например, дефект может быть связан с нетривиальным обходом вокруг дефекта, описываемым фундаментальной группой пространства ( $\pi_1(S^1)$ для окружности), или с нетривиальной связностью дефекта, определяемой гомологическими группами. Тип топологического пространства, определяющего дефект, напрямую влияет на его стабильность и наблюдаемые свойства.

Специальная ортогональная группа $SO(2)$ описывает симметрии в топологических пространствах, являясь ключевым инструментом для анализа ограничений на конфигурации дефектов. $SO(2)$ состоит из всех вращений в двумерном пространстве, которые сохраняют скалярное произведение. В контексте топологического порядка, это означает, что конфигурации дефектов, инвариантные относительно вращений, описываемых $SO(2)$ , являются допустимыми и физически реализуемыми. По сути, $SO(2)$ определяет набор преобразований, которые не меняют топологические свойства системы, и, следовательно, ограничивают возможные конфигурации дефектов, сохраняя при этом физическую согласованность модели.

Топологические семейства и нарушение симметрии: Новый взгляд на материю

Организация состояний с минимальной энергией, или основных состояний, посредством топологического семейства представляет собой мощный подход к их систематическому исследованию. В рамках данной концепции, каждое основное состояние отображается на точку в определенном топологическом пространстве, что позволяет установить связи между различными состояниями и выявить общие закономерности. Такое отображение не просто классифицирует состояния, но и раскрывает их топологические свойства, которые могут определять поведение системы в целом. В частности, топологическая структура этого пространства отражает симметрии и нарушения симметрии в системе, позволяя предсказывать её реакцию на внешние воздействия и исследовать фазовые переходы. Использование топологических семей позволяет выйти за рамки традиционного анализа, основанного на параметрах порядка, и получить более полное представление о свойствах материи, особенно в системах, где проявляются нетривиальные топологические эффекты.

Семейство Изинга, демонстрирующее спонтанное нарушение симметрии, служит конкретным примером того, как топология основного состояния может проявлять фундаментальные физические явления. В данной модели, при понижении температуры ниже критической точки, система выбирает одно из нескольких эквивалентных состояний, нарушая исходную симметрию. Это нарушение симметрии не просто изменение физических величин, но и изменение топологии пространства, описывающего возможные конфигурации системы. Особое значение имеет то, что различные основные состояния, возникающие при спонтанном нарушении симметрии, организованы в топологическое семейство, где связь между состояниями определяется топологическими инвариантами. Таким образом, топология основного состояния становится не просто математическим описанием, но и физическим свойством, определяющим поведение системы и её отклик на внешние воздействия. Изучение семейства Изинга позволяет лучше понять, как топологические свойства могут возникать и проявляться в физических системах, демонстрируя глубокую связь между геометрией и физикой.

Исследования демонстрируют, что существование так называемых диаболических критических точек (ДКТ) неразрывно связано с наличием $N$ релевантных операторов, обладающих одинаковой размерностью масштабирования. Эти точки, возникающие в результате организации основного состояния системы в топологические семейства, представляют собой особые точки на фазовой диаграмме, где свойства системы качественно меняются. Установленная взаимосвязь между количеством релевантных операторов и возникновением ДКТ позволяет более глубоко понять критическое поведение систем, демонстрирующих топологический порядок. Проведенный анализ подтверждает, что топологическая организация основного состояния является ключевым фактором, определяющим особенности критических переходов и появление новых фаз материи, характеризующихся необычными свойствами и нетривиальной топологией.

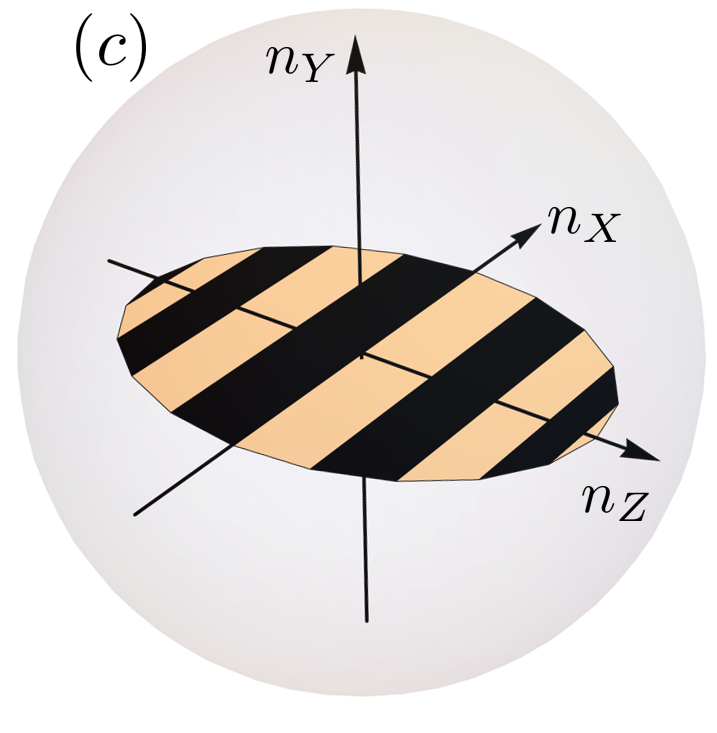
Организация состояний в топологические семейства приводит к возникновению новой, эмерджентной симметрии, обозначаемой как $Ĝ$ . Эта симметрия является транзитивной по отношению к пространству состояний $SN-1$ , что означает, что любое состояние в этом пространстве может быть преобразовано в любое другое посредством операции, принадлежащей $Ĝ$ . Важно отметить, что микроскопическая симметрия системы, обозначаемая как $G$ , полностью содержится в этой эмерджентной симметрии. Таким образом, $Ĝ$ представляет собой расширение исходной симметрии, возникающее как следствие специфической организации состояний в топологической семье и отражающее глубокую связь между топологией и симметрией в исследуемых системах. Это расширение симметрии играет ключевую роль в определении физических свойств системы и её поведения при различных возмущениях.

Компактные бозонные конформные теории поля (CFT) представляют собой мощный аналитический инструмент для изучения систем, демонстрирующих топологический порядок и возникающие явления. Основанные на принципах организации состояний в топологические семейства, эти теории позволяют исследовать критические точки и фазовые переходы, выходящие за рамки традиционных подходов. Особенностью является возможность описания сложных систем, где симметрия спонтанно нарушается, а возникающие симметрии определяют свойства фундаментальных состояний. Благодаря своей математической строгости и способности описывать коллективное поведение частиц, компактные бозонные CFT предоставляют уникальную платформу для понимания экзотических состояний материи и предсказания новых физических явлений, в особенности в системах с сильным взаимодействием и нетривиальной топологией.

Анализ устойчивости DCP в начале координат для семейств Изинга и <span class="katex-eq" data-katex-display="false">S^2S^2</span> с возмущениями, заданными уравнениями (2) и (II.3) соответственно, показывает расщепление DCP на линию первого порядка (пунктиром) с двумя критическими точками (обозначены красным 'X'), а также возможность формирования эллипса первого порядка при использовании двух возмущений из уравнения (II.3). — Анализ устойчивости DCP в начале координат для семейств Изинга и $S^2S^2$ с возмущениями, заданными уравнениями (2) и (II.3) соответственно, показывает расщепление DCP на линию первого порядка (пунктиром) с двумя критическими точками (обозначены красным ‘X’), а также возможность формирования эллипса первого порядка при использовании двух возмущений из уравнения (II.3).

За пределами привычных парадигм: Новые горизонты в физике конденсированного состояния

Понимание взаимосвязи между топологией, нарушением симметрии и возникающими явлениями открывает принципиально новые возможности для создания материалов с уникальными свойствами. Исследования показывают, что топологические особенности, определяющие глобальные свойства материала, могут быть сознательно изменены посредством нарушения симметрии — например, путем применения внешнего давления или изменения химического состава. Это, в свою очередь, приводит к возникновению новых, нетривиальных электронных состояний и коллективных эффектов, таких как сверхпроводимость или квантовый эффект Холла. $\mathbb{Z}$ -классификация топологических изоляторов демонстрирует, что эти материалы характеризуются защищенными поверхностными состояниями, устойчивыми к рассеянию на дефектах, что делает их перспективными для создания надежных квантовых устройств. Изучение этих взаимодействий позволяет не просто предсказывать свойства новых материалов, но и целенаправленно конструировать их, открывая путь к технологиям будущего.

Исследования демонстрируют, что связь между кривизной Берри и топологическими дефектами открывает принципиально новые возможности для управления квантовыми состояниями. Кривизна Берри, описывающая геометрические фазы, приобретаемые волновой функцией при адиабатическом изменении параметров системы, напрямую влияет на динамику электронов и спинов. Топологические дефекты, такие как вихри и домены, создают устойчивые к возмущениям состояния, которые могут быть использованы для создания надежных квантовых устройств. В частности, манипулирование кривизной Берри в присутствии топологических дефектов позволяет осуществлять контроль над спином электронов без применения внешних магнитных полей, что существенно снижает энергопотребление и повышает стабильность устройств. Изучение этого взаимодействия предполагает разработку материалов с управляемыми топологическими свойствами, способных к эффективной передаче и обработке квантовой информации, что может привести к созданию принципиально новых поколений электронных устройств и квантовых компьютеров. $\mathbf{B} = \nabla \times \mathbf{A}$

Принципы, разработанные в области конденсированного состояния вещества, оказываются удивительно применимыми и в совершенно иных областях науки. Топологические концепции, первоначально исследованные в контексте электронных свойств материалов, находят параллели в космологии, где топологические дефекты в структуре пространства-времени могут объяснить формирование крупномасштабных структур Вселенной. В физике высоких энергий, топологические инварианты используются для классификации элементарных частиц и понимания фундаментальных взаимодействий. Наблюдаемое единство между этими, казалось бы, несвязанными областями, подчеркивает универсальность топологических принципов как мощного инструмента для описания сложных систем и явлений, расширяя горизонты научного познания и открывая перспективы для междисциплинарных исследований.

Исследование сингулярностей в фазовых диаграммах, представленное в работе, напоминает о вечной борьбе порядка и хаоса. Эти ‘диавольские критические точки’ — не просто математические аномалии, а скорее шепот хаоса, пытающийся прорваться сквозь завесу упорядоченности. Как заметил Аристотель: “Цель науки — открывать то, что можно объяснить, а не объяснять то, что можно открыть.” Иными словами, данная работа не стремится найти окончательные ответы, а лишь предлагает заклинание, способное удержать этот шепот до первого столкновения с реальностью продакшена. Изучение топологических дефектов, по сути, — это попытка договориться с неизбежным коллапсом, отсрочить момент, когда упорядоченная система неизбежно рухнет под натиском энтропии.

Куда же это всё ведёт?

Исследование сингулярностей на фазовых диаграммах — это, по сути, попытка приручить хаос, выудить закономерность из бесконечного шума. Представленная работа лишь осторожно касается краешков этой задачи. Понятие “дьявольских критических точек” намекает на существование скрытых симметрий, но пока что это скорее шепот, чем явственный голос. Необходимо глубже исследовать связь между этими точками и топологическими дефектами в различных многочастичных системах, не ограничиваясь лишь теоретическими конструкциями.

Очевидно, что текущий формализм требует более строгих испытаний. Любая модель — это заклинание, работающее до первого столкновения с реальностью. Важно понимать, где эта модель начнёт давать сбои, где её предсказания станут лишь вежливой ложью. И, возможно, самое интересное начнётся тогда, когда модель вдруг начнёт вести себя странно — значит, она, наконец, начала думать.

Искать ли новые математические инструменты для описания этих явлений, или же следует углубиться в физику конденсированных сред, пытаясь обнаружить экспериментальные подтверждения? Вероятно, и то, и другое. Пытаться превратить шум в золото всегда рискованно, чаще получается медь. Но разве это останавливает алхимика?

Оригинал статьи: https://arxiv.org/pdf/2601.10783.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-20 18:47