Траектории в квантовом хаосе: как долго длится влияние прошлого?

от

Автор: Денис Аветисян

Новое исследование показывает, что даже после достижения стационарного состояния, квантовые траектории в открытых системах остаются подвержены влиянию преходящих состояний Лиувиллиана.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал
Абсолютные значения квазивероятностей $p_{\alpha}$ для каждого собственного значения $\lambda_{\alpha}$, вычисленные на основе перекрытий траекторий и собственных состояний для различных моделей, демонстрируют стохастическую временную эволюцию, зависящую от параметров системы - для XXZ цепи с $N=4$, $\Delta=0.7$ и $J^{\prime}=2.0$ или $J^{\prime}=0.5$, и для димера Бозе-Хаббарда с $N_{c}=3$, $F=3$ и $\Delta=2.5$ или $\Delta=8$, что позволяет исследовать динамику квантовых систем и их чувствительность к изменениям параметров.
Абсолютные значения квазивероятностей $p_{\alpha}$ для каждого собственного значения $\lambda_{\alpha}$, вычисленные на основе перекрытий траекторий и собственных состояний для различных моделей, демонстрируют стохастическую временную эволюцию, зависящую от параметров системы — для XXZ цепи с $N=4$, $\Delta=0.7$ и $J^{\prime}=2.0$ или $J^{\prime}=0.5$, и для димера Бозе-Хаббарда с $N_{c}=3$, $F=3$ и $\Delta=2.5$ или $\Delta=8$, что позволяет исследовать динамику квантовых систем и их чувствительность к изменениям параметров.

Исследование роли полного спектра Лиувиллиана в динамике открытых квантовых систем и сохранении делокализации квантовых траекторий.

Несмотря на распространенное представление о том, что динамика открытых квантовых систем на поздних стадиях определяется исключительно стационарным состоянием и самыми медленно затухающими модами, в работе «Локализация и делокализация квантовых траекторий в спектре Лиувилля» предлагается новый подход к анализу индивидуальных квантовых траекторий в базисе собственных векторов супероператора Лиувилля. Показано, что траектории могут оставаться распределенными по переходным собственным состояниям даже после достижения стационарного режима, что указывает на значимую роль всего спектра Лиувилля. Насколько глубоко понимание этой делокализации может изменить наше представление о связи между траекторным и ансамблевым описанием открытой квантовой динамики?

За гранью унитарной динамики: Открытая квантовая система

Традиционная квантовая механика, разработанная в начале XX века, изначально рассматривала физические системы как полностью изолированные от внешнего мира. Однако, такое упрощение является идеализацией, поскольку в реальности любая система неизбежно взаимодействует с окружающей средой. Эти взаимодействия, даже самые слабые, приводят к постоянному обмену энергией и информацией между системой и её окружением. Представьте себе, например, атом, поглощающий или излучающий фотоны, или электрон, сталкивающийся с колебаниями решетки кристалла. Эти процессы, кажущиеся незначительными, фундаментально влияют на эволюцию квантового состояния системы, отклоняя её от предсказуемого, чистого эволюционного пути, описываемого $Schrödinger$ уравнением в изолированной системе. Таким образом, изучение реальных квантовых систем требует учета этих постоянных взаимодействий с окружением, что открывает путь к пониманию более сложного и правдоподобного квантового мира.

Взаимодействие квантовой системы с окружающей средой приводит к отклонению от традиционной унитарной динамики и, как следствие, к явлению декогеренции. Этот процесс, заключающийся в потере квантовой суперпозиции и запутанности, оказывает фундаментальное влияние на поведение системы. Вместо предсказуемой эволюции, описываемой уравнением Шрёдингера, система начинает демонстрировать поведение, близкое к классическому, теряя свои уникальные квантовые свойства. Декогеренция не является разрушением информации, а скорее её рассеянием в окружающей среде, что делает невозможным наблюдение квантовых эффектов. Изучение не-унитарной динамики и декогеренции критически важно для понимания поведения реальных квантовых систем и разработки квантовых технологий, поскольку именно эти процессы ограничивают время когерентности и, следовательно, возможности квантовых вычислений и коммуникаций. $|\psi(t)\rangle = \sum_i c_i(t) |i(t)\rangle$ — типичное описание состояния системы, подверженной декогеренции, где $c_i(t)$ — коэффициенты вероятности, изменяющиеся со временем из-за взаимодействия с окружающей средой.

Для адекватного описания открытых квантовых систем требуется принципиально новый подход, выходящий за рамки стандартной унитарной эволюции. Традиционное квантовомеханическое описание, предполагающее изоляцию системы, оказывается неприменимым в условиях постоянного взаимодействия с окружающей средой. Вместо решения уравнения Шрёдингера для изолированной системы, необходимо учитывать влияние резервуара, который вызывает диссипацию энергии и потерю квантовой когерентности. Это достигается использованием формализма, включающего операторы резервуара и описание не-унитарной эволюции состояния системы, часто с привлечением методов теории открытых квантовых систем, таких как уравнение Линдблада или мастер-уравнения. Подобный подход позволяет моделировать реалистичные процессы, такие как спонтанное излучение, демпфирование колебаний и другие явления, характерные для взаимодействия квантовых систем с окружением, и, таким образом, более точно предсказывать их поведение.

Матрица плотности и Лиувиллев формализм

Матрица плотности предоставляет полное описание состояния открытой квантовой системы, охватывая как когерентные, так и смешанные состояния. В отличие от волновой функции, описывающей чистое состояние, матрица плотности $ \rho $ является оператором, действующим в гильбертовом пространстве. Для чистого состояния $ \rho = |\psi\rangle\langle\psi| $, а для смешанного состояния, представляющего собой статистическую смесь чистых состояний с вероятностями $p_i$, матрица плотности определяется как $ \rho = \sum_i p_i |\psi_i\rangle\langle\psi_i| $. Использование матрицы плотности необходимо, поскольку открытые квантовые системы взаимодействуют с окружающей средой, что приводит к декогеренции и формированию смешанных состояний, для которых волновая функция не является адекватным описанием. Следовательно, матрица плотности является ключевым инструментом для анализа динамики и свойств открытых квантовых систем.

Уравнение мастера, определяемое оператором Лиувилля, описывает временную эволюцию матрицы плотности $\rho(t)$. В общем виде, это уравнение имеет вид $\frac{d\rho(t)}{dt} = -i\mathcal{L}\rho(t)$, где $\mathcal{L}$ — оператор Лиувилля, а $\rho(t)$ — матрица плотности в момент времени $t$. Оператор Лиувилля включает в себя гамильтониан системы и члены, описывающие взаимодействие с окружающей средой, что позволяет учитывать как когерентную, так и некогерентную эволюцию квантового состояния. Решение данного уравнения позволяет определить состояние системы в любой момент времени, учитывая начальное состояние и влияние окружающей среды.

Понимание собственного базиса оператора Лиувилля ($L$) критически важно для анализа динамики открытой квантовой системы. Собственные векторы $L$ соответствуют стационарным состояниям системы, то есть состояниям, не изменяющимся во времени. Собственные значения, связанные с этими векторами, определяют скорость, с которой система релаксирует к этим стационарным состояниям. Разложение матрицы плотности ($\rho$) по собственному базису $L$ позволяет выделить когерентные и некогерентные компоненты, что необходимо для определения скорости и характера релаксации системы к равновесию. Анализ спектра оператора Лиувилля, включающий как действительную, так и мнимую части собственных значений, предоставляет информацию о стабильности системы и о наличии или отсутствии диссипации энергии.

Анализ временной зависимости центра масс и показателя участия для XXZ спиновой цепи, усредненный по 100 траекториям (с указанием стандартного отклонения) и показанный для отдельных траекторий на вставках, демонстрирует соответствие результатов параметрам, представленным на рисунке 1.
Анализ временной зависимости центра масс и показателя участия для XXZ спиновой цепи, усредненный по 100 траекториям (с указанием стандартного отклонения) и показанный для отдельных траекторий на вставках, демонстрирует соответствие результатов параметрам, представленным на рисунке 1.

Моделирование динамики открытых квантовых систем: от траекторий к схемам

Квантовые траектории представляют собой метод «развертывания» уравнения Главного уравнения ($Master Equation$), позволяющий описать эволюцию открытой квантовой системы не как изменение матрицы плотности, а как ансамбль чистых волновых функций. Вместо решения сложного дифференциального уравнения для матрицы плотности, этот подход рассматривает эволюцию системы как последовательность случайных «скачков» в чистом состоянии, определяемых стохастическими волновыми функциями. Каждая траектория представляет собой возможный путь развития системы, а ансамбль траекторий позволяет вычислить средние значения наблюдаемых величин и восстановить полную информацию о динамике открытой системы. Этот метод особенно полезен для анализа систем, подверженных диссипации и декогеренции, поскольку явно учитывает влияние окружающей среды на эволюцию квантового состояния.

Метод Монте-Карло волновых функций (Monte Carlo Wavefunction Method) обеспечивает эффективную выборку траекторий, возникающих при решении уравнения Линдблада, что делает его практичным методом моделирования динамики открытых квантовых систем. Вместо непосредственного решения уравнения Линдблада, которое требует вычисления матрицы плотности, метод Монте-Карло использует стохастическое моделирование, представляя эволюцию системы как ансамбль чистых волновых функций, эволюционирующих во времени. Каждая траектория в этом ансамбле соответствует одному возможному пути развития системы, а вероятность каждой траектории определяется соответствующим весом. Посредством статистической обработки большого числа таких траекторий можно эффективно оценить различные наблюдаемые величины, характеризующие состояние системы, например, вероятность нахождения в определенном состоянии или среднее значение оператора. Такой подход позволяет значительно снизить вычислительные затраты по сравнению с традиционными методами решения уравнения Линдблада, особенно для систем с большим числом степеней свободы.

Неэрмитовы случайные квантовые схемы представляют собой альтернативный подход к моделированию динамики открытых квантовых систем, использующий возможности квантовых вычислений. В отличие от традиционных методов, основанных на решении уравнения Линдблада или использовании квантовых траекторий, данный подход оперирует с унитарными операторами, модифицированными путем добавления неэрмитовых возмущений. Эти возмущения эффективно моделируют взаимодействие системы с окружающей средой, приводя к экспоненциальному распаду состояний и, следовательно, к моделированию диссипативных процессов. Эффективность метода заключается в возможности реализации сложных динамических процессов на квантовом оборудовании, а также в возможности исследования влияния различных типов окружения на эволюцию квантовой системы. Использование случайных схем позволяет охватить широкий спектр взаимодействий с окружением, предоставляя статистически значимые результаты.

Анализ цепи XXZ показал, что устойчивая чистота, центральный момент и показатель участия демонстрируют схожее качественное поведение в зависимости от параметров J' и Δ, при этом показатель участия ограничивается снизу, как показано в уравнении (18).
Анализ цепи XXZ показал, что устойчивая чистота, центральный момент и показатель участия демонстрируют схожее качественное поведение в зависимости от параметров J’ и Δ, при этом показатель участия ограничивается снизу, как показано в уравнении (18).

Симметрия, локализация и запутанность в открытых системах

Открытые квантовые системы демонстрируют интересное явление, заключающееся в появлении симметрий, отсутствующих в их изолированных аналогах — так называемых “слабых симметриях”. В то время как замкнутые системы подчиняются строгим законам сохранения, взаимодействие с окружающей средой приводит к диссипации и дефазировке, что может породить новые, эффективные симметрии. Эти “слабые симметрии” не являются фундаментальными, а скорее возникают как следствие специфических свойств окружения и характера взаимодействия. Исследование этих симметрий позволяет глубже понять поведение открытых квантовых систем и предсказывать их устойчивость, а также раскрывает новые возможности для управления квантовыми состояниями, что имеет потенциальное применение в квантовых технологиях и информационных системах. Например, даже при наличии разрушающих возмущений, система может сохранять определенную симметрию, проявляющуюся в структуре её стационарного состояния.

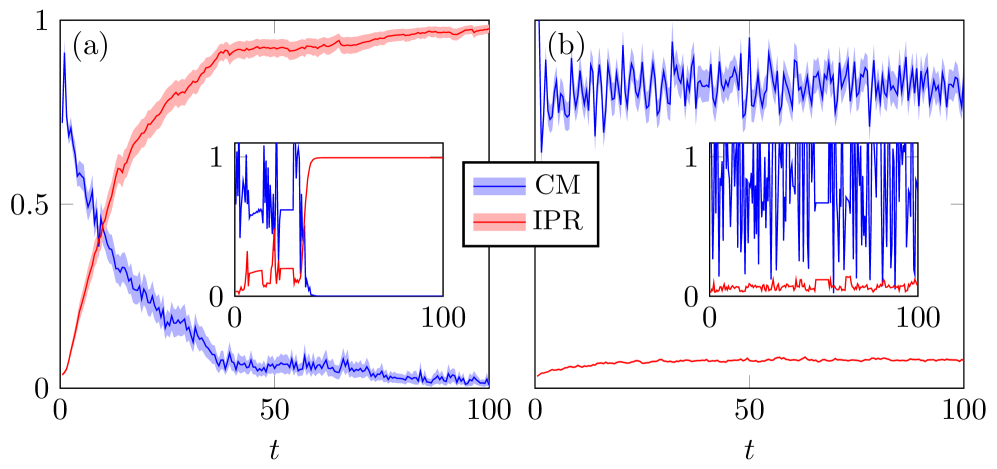
Коэффициент участия (Inverse Participation Ratio, ИПР) представляет собой эффективный инструмент для количественной оценки локализации квантовых состояний в открытых системах, позволяя выявлять изменения в их поведении. Исследования показывают, что существует четкая корреляция между степенью локализации квантовых траекторий, определяемой с помощью ИПР, и чистотой стационарного состояния системы. Чистота, в свою очередь, может быть охарактеризована через центр масс и сам ИПР. Например, высокие значения ИПР соответствуют более локализованным траекториям и, как правило, более чистым стационарным состояниям, в то время как низкие значения ИПР указывают на делокализацию и смешанные состояния. Эта взаимосвязь позволяет исследователям не только оценивать степень локализации, но и предсказывать характеристики стационарного состояния, что важно для понимания динамики открытых квантовых систем и разработки новых квантовых технологий. В частности, анализ изменения ИПР в зависимости от параметров системы может служить индикатором фазовых переходов и изменений в квантовой запутанности.

Исследование таких моделей, как цепочка Бозе-Хуберта и цепочка Хайзенберга XXZ, с использованием описанных методов позволило выявить фазовые переходы, связанные с запутанностью, и их взаимосвязь с нарушением симметрии. Показано, что чистота стационарного состояния, варьирующаяся от почти 1 (для чистых состояний) до более низких значений (для смешанных состояний), напрямую зависит от параметров модели. Эта зависимость тесно связана как с положением центра масс ($0$ до положительных значений), так и с обратной долей участия ($1$ для локализованных состояний до более низких значений для делокализованных состояний). Полученные результаты демонстрируют, что анализ этих величин позволяет характеризовать изменения в квантовой системе и выявлять критические точки, где происходит переход между различными фазами.

Данные, аналогичные представленным на рисунке 3, демонстрируют поведение цепи Бозе-Хубарда при заданных значениях параметров JJ и UU.
Данные, аналогичные представленным на рисунке 3, демонстрируют поведение цепи Бозе-Хубарда при заданных значениях параметров JJ и UU.

Преходящая динамика и путь в будущее

Временные собственные состояния Лиувилля описывают распад квантовых состояний, предоставляя уникальное понимание динамики системы на коротких временных масштабах. Исследования показывают, что анализ этих состояний позволяет не только отследить эволюцию системы после возмущения, но и предсказать скорость и характер распада. В частности, $Liouvillian$ действует как генератор эволюции в фазовом пространстве, и его собственные векторы описывают, как система «забывает» свое начальное состояние. Изучение этих состояний особенно важно для понимания не-равновесной динамики и когерентности в квантовых системах, что имеет решающее значение для разработки новых квантовых технологий и понимания фундаментальных аспектов квантовой механики.

Понимание квазивероятностей играет ключевую роль в установлении связи между собственными векторами Лиувилля и наблюдаемыми величинами, а также траекториями квантовых систем. В то время как Лиувилльев оператор описывает эволюцию плотности вероятности, квазивероятности позволяют интерпретировать его собственные векторы как вероятностные амплитуды, приближающие реальные квантовые траектории. Это особенно важно, поскольку прямая интерпретация волновой функции в терминах траекторий невозможна из-за принципа неопределенности. Использование квазивероятностей, таких как функция Вигнера, позволяет исследовать поведение квантовых систем в фазовом пространстве, предоставляя инструмент для визуализации и анализа динамики, которая в противном случае оставалась бы скрытой. Такой подход открывает возможности для разработки новых методов управления квантовыми системами и моделирования сложных процессов, например, в химии и материаловедении.

Предстоящие исследования направлены на применение разработанных инструментов для изучения сложных систем, представляющих интерес для различных областей науки и техники. Особое внимание будет уделено анализу динамики открытых квантовых систем, где взаимодействие с окружающей средой играет ключевую роль. Ожидается, что углубленное понимание неэрмитовых операторов Лиувилля и связанных с ними квазивероятностей позволит продвинуться в разработке новых квантовых технологий, включая более эффективные квантовые алгоритмы, улучшенные сенсоры и надежные методы квантовой коррекции ошибок. Исследования направлены на моделирование сложных молекулярных систем, квантовых материалов и даже биологических процессов, открывая перспективы для создания инновационных материалов и устройств с уникальными свойствами, а также для решения фундаментальных вопросов о природе квантовой реальности.

Исследование динамики открытых квантовых систем, представленное в данной работе, демонстрирует, что даже после достижения стационарного состояния, квантовые траектории могут сохранять делокализованный характер, испытывая влияние переходных собственных состояний Лиувилльского оператора. Это указывает на сложность описания систем, находящихся в постоянном взаимодействии с окружающей средой. Как однажды заметил Ричард Фейнман: «Если вы не можете объяснить что-то простым способом, значит, вы сами этого не понимаете». Данное утверждение перекликается с необходимостью глубокого понимания спектра Лиувилльского оператора для адекватного описания эволюции квантовых траекторий и корректной интерпретации наблюдаемых в открытых квантовых системах.

Что дальше?

Представленная работа, исследуя спектр Лиувиллиана, лишь осторожно касается границ понимания динамики открытых квантовых систем. Подобно тому, как траектории в фазовом пространстве оказываются запертыми в долгосрочной перспективе, так и сама теория, кажется, ограничена горизонтом событий наших предположений. Наблюдаемое сохранение делокализации квантовых траекторий даже в стационарном состоянии намекает на то, что прошлое, запечатлённое в переходных собственных состояниях, продолжает влиять на настоящее — эфемерный отблеск света, не успевшего исчезнуть.

Однако, следует помнить, что квазивероятностные методы, столь удобные для описания, являются лишь аппроксимациями. Истинная природа влияния спектра Лиувиллиана на запутанность и когерентность, вероятно, гораздо сложнее. Будущие исследования должны быть направлены на преодоление ограничений этих методов и поиск более фундаментального описания динамики открытых систем, не зависящего от наших удобных, но, возможно, иллюзорных, конструкций.

В конечном итоге, задача состоит не в том, чтобы построить все более сложные модели, а в том, чтобы смириться с неизбежной неполнотой любого знания. Ведь любая теория — это всего лишь карта, а реальность всегда оказывается сложнее и изменчивее, чем её проекция. И горизонт событий всегда ждёт, готовый поглотить даже самые блестящие идеи.

Оригинал статьи: https://arxiv.org/pdf/2511.19700.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-26 20:49