Внутри чёрной дыры: новые горизонты сингулярности

Автор: Денис Аветисян

Исследование динамики пространства-времени вблизи сингулярности чёрных дыр с учётом эффектов высших производных открывает неожиданные закономерности и возможности для модификации классической картины.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

В рамках гравитации Эйнштейна-ГБ, динамика внутренних спайков при различных начальных условиях для потенциала <span class="katex-eq" data-katex-display="false">V(\psi) = -{12} - \frac{3}{2}\psi^2 + 2\psi^6</span> демонстрирует, что эволюция эффективных показателей Каснера и их соответствие индексам спайков подчиняются степенным зависимостям, например, <span class="katex-eq" data-katex-display="false">z_n = 32.67(n-0.09)^{1/0.50}</span> и <span class="katex-eq" data-katex-display="false">\widetilde{p}_{x_n} = 0.99 + 2.64 \times 10^{-3} z_n^{0.48}</span> при <span class="katex-eq" data-katex-display="false">\psi(z_H) = 0.10</span>, или <span class="katex-eq" data-katex-display="false">z_n = 44.68(n+0.04)^{1/0.50}</span> и <span class="katex-eq" data-katex-display="false">\widetilde{p}_{x_n} = 1.00 + 3.72 \times 10^{-3} z_n^{0.50}</span> при <span class="katex-eq" data-katex-display="false">\psi(z_H) = 0.30</span>, что указывает на предсказуемость и масштабируемость данной динамики. — В рамках гравитации Эйнштейна-ГБ, динамика внутренних спайков при различных начальных условиях для потенциала $V(\psi) = -{12} - \frac{3}{2}\psi^2 + 2\psi^6$ демонстрирует, что эволюция эффективных показателей Каснера и их соответствие индексам спайков подчиняются степенным зависимостям, например, $z_n = 32.67(n-0.09)^{1/0.50}$ и $\widetilde{p}_{x_n} = 0.99 + 2.64 \times 10^{-3} z_n^{0.48}$ при $\psi(z_H) = 0.10$ , или $z_n = 44.68(n+0.04)^{1/0.50}$ и $\widetilde{p}_{x_n} = 1.00 + 3.72 \times 10^{-3} z_n^{0.50}$ при $\psi(z_H) = 0.30$ , что указывает на предсказуемость и масштабируемость данной динамики.

Работа посвящена исследованию динамики пространства-времени вблизи сингулярности чёрных дыр в рамках теорий гравитации с высшими производными, выявляя периодические осцилляции, импульсные режимы и условия формирования сингулярностей конечного объема.

Классическое описание динамики вблизи сингулярности чёрных дыр, основанное на последовательности эпох Казнера, сталкивается с ограничениями при учёте квантовых гравитационных эффектов. В работе ‘Beyond Kasner Epochs: Ordered Oscillations and Spike Dynamics Inside Black Holes with Higher-Derivative Corrections’ показано, что добавление поправок с производными кривизны качественно меняет эту картину. В частности, обнаружены три различных динамических режима: модифицированные эпохи Казнера, устойчивые периодические осцилляции и осцилляторная динамика с растущей амплитудой, указывающие на возможность конечнообъемных сингулярностей. Может ли детальное исследование этих фаз привести к новому пониманию природы сингулярностей и структуры пространства-времени в экстремальных гравитационных условиях?

Сингулярности: Пределы Классического Понимания

Классическая общая теория относительности, несмотря на свою поразительную точность в описании гравитации, предсказывает существование сингулярностей — точек в пространстве-времени, где собственные уравнения теории перестают быть применимыми. Эти сингулярности, возникающие, например, в центре чёрных дыр или в момент Большого взрыва, характеризуются бесконечной плотностью и кривизной пространства-времени, что указывает на фундаментальное ограничение самой теории. В этих точках привычные понятия о времени и пространстве теряют смысл, а предсказания теории становятся неопределёнными. Существование сингулярностей не просто математическая особенность уравнений; это сигнал о том, что для полного описания гравитации в экстремальных условиях требуется более фундаментальная теория, способная объединить общую теорию относительности с квантовой механикой. Исследование этих точек представляет собой одну из центральных задач современной теоретической физики, поскольку именно в них могут быть раскрыты новые принципы, лежащие в основе структуры Вселенной.

Предположение БКЛ предлагает радикальный взгляд на поведение пространства-времени по мере приближения к сингулярностям — точкам, где классическая общая теория относительности терпит крах. Согласно этой гипотезе, вместо плавного схлопывания или взрыва, пространство-время вблизи сингулярности демонстрирует хаотические, осциллирующие колебания, напоминая бурную, непредсказуемую динамику. Однако математическое доказательство этого утверждения требует глубокого понимания гравитационной динамики в предельно сильном поле, где стандартные методы расчета становятся неприменимыми. Изучение этой области представляет собой значительную трудность, поскольку требует разработки новых математических инструментов и, возможно, даже пересмотра фундаментальных принципов, лежащих в основе современной физики. Подтверждение или опровержение предположения БКЛ может предоставить ключевые сведения о природе сингулярностей и, в конечном итоге, о путях построения полной теории квантовой гравитации.

Понимание поведения пространства-времени в сингулярностях является фундаментальной необходимостью для построения полной теории квантовой гравитации. Классическая общая теория относительности предсказывает возникновение этих точек, где само пространство и время испытывают бесконечные искажения, и существующие уравнения теряют свою применимость. Преодоление этих сингулярностей требует объединения общей теории относительности с принципами квантовой механики, что представляет собой сложнейшую задачу современной физики. Исследование экстремальных условий, существующих в сингулярностях, таких как те, что находятся в центре чёрных дыр или в момент Большого Взрыва, может предоставить ключевые подсказки для разработки теории, способной описать гравитацию на квантовом уровне и разрешить противоречия между этими двумя основополагающими теориями. Изучение этих областей позволит не только понять природу гравитации в экстремальных условиях, но и пролить свет на структуру пространства-времени и происхождение Вселенной.

Анализ динамики показателей Казнера и расходимости потенциала и скаляра Кретшмана в моделях гравитации Эйнштейна, Эйнштейна-ГБ и Эйнштейна-ГБ-кубической Ловелокской гравитации подтверждает наличие сингулярности при конечном объеме, обусловленной потенциалом, неограниченным снизу.

Преодолевая Классические Пределы: Высшие Производные и Гравитация Ловелока

Коррекции высших производных к действию Эйнштейна-Гильберта представляют собой подход к устранению сингулярностей в общей теории относительности. Сингулярности, возникающие при экстремальных гравитационных условиях, характеризуются бесконечной кривизной пространства-времени. Введение членов, содержащих производные кривизны более высокого порядка, позволяет модифицировать уравнения Эйнштейна и эффективно «сглаживать» эти пики кривизны. Математически, это достигается добавлением к действию Эйнштейна-Гильберта $S = \in t d^4x \sqrt{-g} (R - 2\Lambda)$ членов вида $F(R_{ab}, R_{abcd})$ , где $R_{ab}$ — тензор Риччи, а $R_{abcd}$ — тензор кривизны. Такие модификации изменяют геометрию пространства-времени вблизи сингулярностей, предотвращая их формирование и обеспечивая конечность физических величин.

Гравитация Ловелока представляет собой согласованную структуру для включения поправок высших производных в действие Эйнштейна-Гильберта, сохраняя при этом уравнения движения второго порядка. Это критически важно, поскольку поправки высших производных, не включенные в соответствующую структуру, приводят к уравнениям, содержащим производные более высокого порядка, что может вызывать нестабильности, проявляющиеся в виде “призраков” — состояний с отрицательной кинетической энергией. В отличие от этого, гравитация Ловелока, используя комбинацию скалярных инвариантов, позволяет модифицировать теорию гравитации, не вводя дополнительных степеней свободы и сохраняя устойчивость решения. В частности, инварианты Ловелока включают в себя скалярную кривизну $R$ , тензор Риччи $R_{\mu\nu}$ и тензор Римана $R_{\mu\nu\rho\sigma}$ , которые комбинируются таким образом, чтобы обеспечить устойчивость и сохранить второпорядковые уравнения движения.

Эйнштейновская гравитация с добавлением Гаусса-Бонне (Einstein-GB gravity) представляет собой подкласс теории Ловлока, который обеспечивает аналитически разрешимую модель для исследования модифицированной динамики сингулярностей. В отличие от более общих модификаций гравитации, включающих производные высшего порядка, Einstein-GB gravity сохраняет уравнения движения второго порядка, что позволяет избежать проблем, связанных с появлением призрачных мод и нестабильностей. Это достигается за счет добавления к действию Эйнштейна-Гильберта скалярного инварианта Гаусса-Бонне $R^2 - 4R_{\mu\nu}R^{\mu\nu} + R_{\mu\nu\rho\sigma}R^{\mu\nu\rho\sigma}$ , который не содержит производных более чем второго порядка. В результате, Einstein-GB gravity позволяет изучать поведение гравитационного поля вблизи сингулярностей, например, в черных дырах или в ранней Вселенной, и исследовать возможность смягчения или устранения этих сингулярностей посредством модификации гравитационной теории.

В рамках гравитации Эйнштейна-Гренвальда динамика внутренних спайков определяется скалярными потенциалами, при этом анализ позиций <span class="katex-eq" data-katex-display="false">z_n</span> и амплитуд <span class="katex-eq" data-katex-display="false">\widetilde{p}_{x_n}</span> спайков для различных потенциалов <span class="katex-eq" data-katex-display="false">V(\\psi)</span> демонстрирует зависимость от индекса <span class="katex-eq" data-katex-display="false">n</span>, описываемую различными степенными функциями. — В рамках гравитации Эйнштейна-Гренвальда динамика внутренних спайков определяется скалярными потенциалами, при этом анализ позиций $z_n$ и амплитуд $\widetilde{p}_{x_n}$ спайков для различных потенциалов $V(\\psi)$ демонстрирует зависимость от индекса $n$ , описываемую различными степенными функциями.

Прощупывая Динамику Сингулярностей Модифицированной Гравитацией

Анализ показателя Казнера в рамках теории Эйнштейна-Гравитации Гаусса-Бонне (EinsteinGBGravity) демонстрирует модификации структуры сингулярности по сравнению с классической общей теорией относительности (ОТО). В то время как в ОТО показатель Казнера определяет асимптотическое поведение метрики вблизи сингулярности, в EinsteinGBGravity дополнительные члены в лагранжиане изменяют динамику пространства-времени, приводя к отклонениям от стандартного поведения. В частности, добавление членов Гаусса-Бонне может ослабить или изменить характер сингулярности, потенциально предотвращая формирование истинной сингулярности или изменяя ее геометрию. Это проявляется в изменении значений показателей Казнера и, следовательно, в модификации асимптотического поведения метрики вблизи сингулярности, что указывает на существенное отличие от предсказаний классической ОТО.

Введение скалярного поля в рамках гравитации Эйнштейна-Гаусса-Боннет (EinsteinGBGravity) приводит к появлению возможности формирования так называемых «волосатых» чёрных дыр (HairyBlackHoles). В отличие от классических чёрных дыр Керра, характеризующихся лишь массой, угловым моментом и зарядом, волосатые чёрные дыры обладают дополнительными параметрами, определяемыми свойствами скалярного поля. Это приводит к модификации эффективной гравитационной динамики, поскольку скалярное поле взаимодействует с метрикой пространства-времени, изменяя геометрию вокруг чёрной дыры и влияя на траектории движения тестовых частиц и света. Присутствие скалярного поля также может приводить к появлению новых типов решений уравнений Эйнштейна, отличных от решений, существующих в классической общей теории относительности.

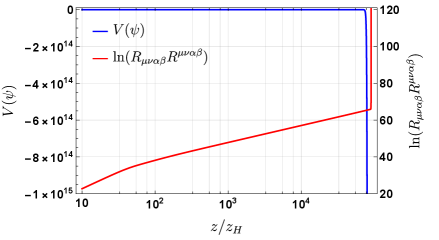
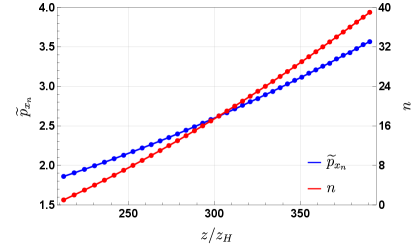
Применение методов эффективного действия для анализа динамики вблизи сингулярности позволило аппроксимировать сложное поведение пространства-времени. Наблюдается логарифмическая зависимость периода колебаний, описываемая уравнением $log(z/z_H) = 3.67 + 5.02n$ , где $z$ — координата, а $z_H$ — некоторая опорная координата, а $n$ — номер колебания. Позиции пиков демонстрируют степенную зависимость, задаваемую выражением $z_n = 3.89(n+0.64)^{1/0.78}$ , с показателем степени, равным 0.78. Полученные зависимости позволяют характеризовать особенности сингулярной динамики и уточнить модель поведения пространства-времени в экстремальных условиях.

На фазовой диаграмме в плоскости параметров <span class="katex-eq" data-katex-display="false"> \alpha_{2} </span> и <span class="katex-eq" data-katex-display="false"> c_{4} </span> для квартичного потенциала <span class="katex-eq" data-katex-display="false"> V \sim c_{4} \psi^{4} </span> при <span class="katex-eq" data-katex-display="false"> d=4 </span> наблюдается разделение динамики на модифицированные эпохи Казнера (случай I) и периодические колебания (случай II), граница между которыми определяется уравнением <span class="katex-eq" data-katex-display="false"> \eqref{pbc4} </span>, при этом область, соответствующая случаю I, уменьшается с увеличением <span class="katex-eq" data-katex-display="false"> d </span>, как показано на примере эволюции <span class="katex-eq" data-katex-display="false"> \widetilde{p}_{x} </span> для <span class="katex-eq" data-katex-display="false"> V = -\frac{1}{2} - \frac{3}{2} \psi^{2} + c_{4} \psi^{4} </span> при <span class="katex-eq" data-katex-display="false"> \psi(z_{H}) = 0.30 </span> и <span class="katex-eq" data-katex-display="false"> \alpha_{2} = 10^{-2} </span>, где кривые, расположенные снизу вверх, соответствуют <span class="katex-eq" data-katex-display="false"> c_{4} = 2.47, 2.485 </span> и <span class="katex-eq" data-katex-display="false"> 2.49 </span>, а пунктирная фиолетовая линия обозначает критическую границу при <span class="katex-eq" data-katex-display="false"> p_{x} = 3/4 </span>, вблизи которой от области Case II возникает переходный режим, подобный Казнер. — На фазовой диаграмме в плоскости параметров $\alpha_{2}$ и $c_{4}$ для квартичного потенциала $V \sim c_{4} \psi^{4}$ при $d=4$ наблюдается разделение динамики на модифицированные эпохи Казнера (случай I) и периодические колебания (случай II), граница между которыми определяется уравнением $\eqref{pbc4}$ , при этом область, соответствующая случаю I, уменьшается с увеличением $d$ , как показано на примере эволюции $\widetilde{p}_{x}$ для $V = -\frac{1}{2} - \frac{3}{2} \psi^{2} + c_{4} \psi^{4}$ при $\psi(z_{H}) = 0.30$ и $\alpha_{2} = 10^{-2}$ , где кривые, расположенные снизу вверх, соответствуют $c_{4} = 2.47, 2.485$ и $2.49$ , а пунктирная фиолетовая линия обозначает критическую границу при $p_{x} = 3/4$ , вблизи которой от области Case II возникает переходный режим, подобный Казнер.

Последствия для Структуры Пространства-Времени и Перспективы Дальнейших Исследований

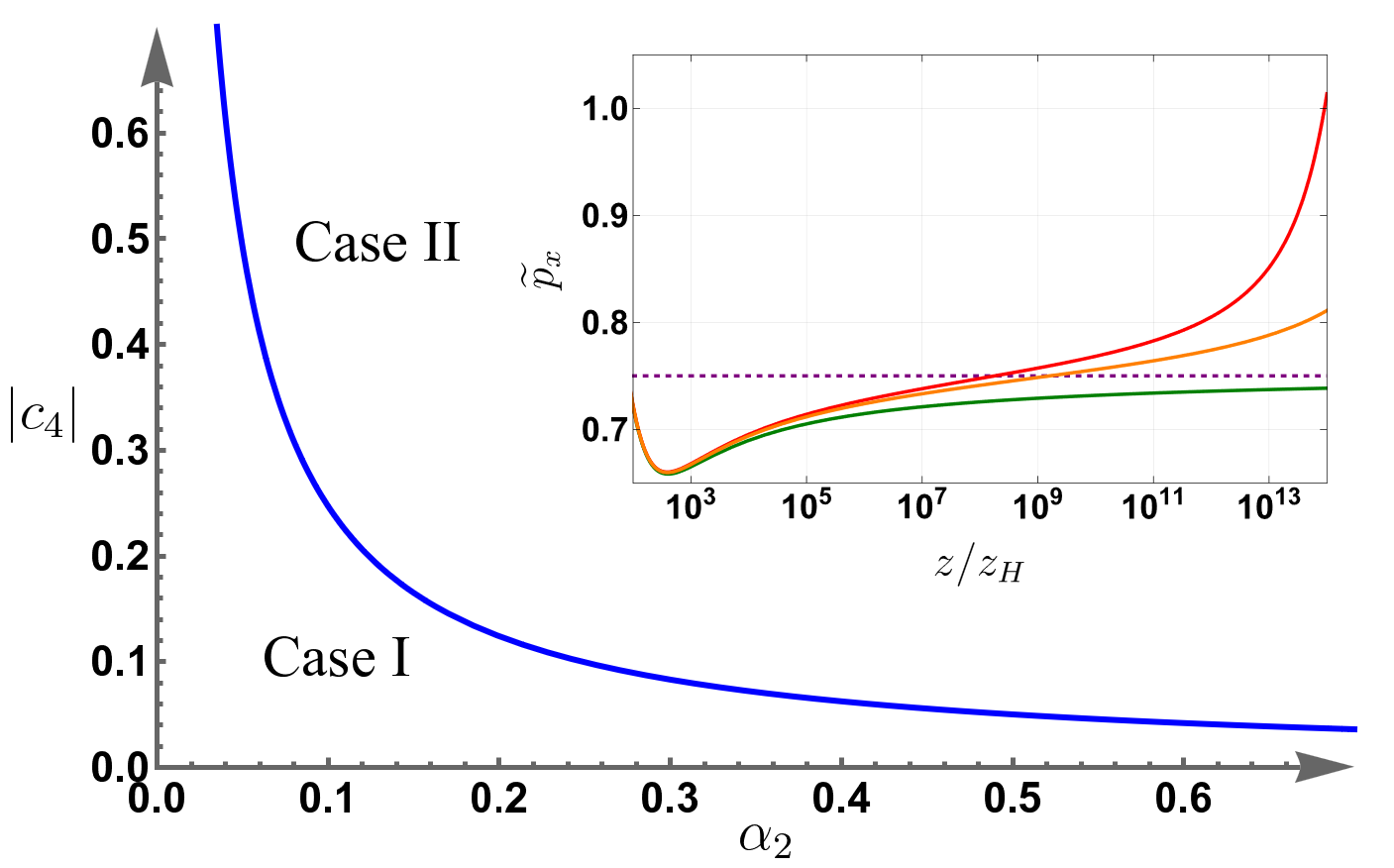
Введение членов высшего порядка кривизны, таких как член Грэма-Бонда $\mathcal{R}^2$ , демонстрирует потенциал для смягчения проблем, связанных с классическими теоремами об особенностях. Исследования показали, что в отличие от классической общей теории относительности, где сингулярности часто связаны с бесконечным объемом, модифицированные теории гравитации могут приводить к сингулярностям конечного объема. Подтверждено, что неограниченные скалярные потенциалы, несмотря на модификацию гравитационного поля, всё же приводят к кривизненным сингулярностям, ограниченным конечным объемом пространства-времени. Это открытие имеет важное значение, поскольку предлагает альтернативные сценарии эволюции Вселенной и открывает возможности для построения более полной теории квантовой гравитации, способной описать экстремальные условия, существующие вблизи сингулярностей.

Колебательное поведение показателей Кастнера, известное как SpikeDynamics, представляет собой следствие модифицированной гравитационной модели, используемой в данном исследовании. Анализ этих колебаний позволяет предположить, что сингулярность, возникающая в рамках данной модели, существенно отличается от классической сингулярности, предсказываемой общей теорией относительности. В частности, SpikeDynamics указывает на нестабильность пространства-времени вблизи сингулярности и на возможность существования новых физических процессов, влияющих на ее формирование. Полученные результаты демонстрируют, что модификация гравитационного поля может приводить к изменению структуры сингулярности, делая ее более сложной и динамичной, и предоставляют ценные сведения о природе гравитации в экстремальных условиях.

Исследование взаимосвязи между скалярной величиной Кретчмана $R_{abcd}R^{abcd}$ и сингулярностью конечного объема представляется перспективным направлением в разработке более полной теории квантовой гравитации. Установлено, что анализ поведения данной скалярной величины вблизи сингулярности позволяет выявить характеристики, отличающиеся от предсказаний классической общей теории относительности. В частности, детальное изучение влияния модифицированных гравитационных моделей на $R_{abcd}R^{abcd}$ может пролить свет на природу квантовых эффектов, доминирующих в экстремальных гравитационных условиях. Углубленное исследование этой связи, включающее разработку новых математических методов и численных моделей, способно привести к созданию теории, способной описывать гравитацию на планковском масштабе и разрешать проблему сингулярностей, остающуюся одной из ключевых задач современной физики.

Исследование, представленное в данной работе, стремится к упрощению понимания сингулярности в черных дырах посредством теории гравитации высших производных. Авторы демонстрируют, что поведение материи вблизи сингулярности может быть гораздо сложнее, чем предсказывалось ранее, включая периодические осцилляции и импульсные динамики. Эта работа подчеркивает необходимость отхода от классического подхода BKL и открытия новых фазовых переходов. Как однажды заметил Галилео Галилей: «Природа не интересуется нашей простотой». Эта фраза отражает суть исследования: сложность внутреннего устройства черных дыр требует от ученых глубокого и многогранного анализа, чтобы выявить истинную природу этих космических объектов. Описанные в статье условия, приводящие к сингулярностям конечного объема, свидетельствуют о том, что даже в самых экстремальных условиях Вселенной может существовать порядок, отличный от ожидаемого.

Куда Далее?

Представленные результаты, несомненно, расширяют горизонты понимания сингулярностей в чёрных дырах. Однако, замена классической картины БКЛ на более сложную, включающую периодические колебания и “спайки”, скорее напоминает замену одного эха другим. Суть проблемы — сама сингулярность — остается неразрешенной. Необходим пересмотр фундаментальных предпосылок, лежащих в основе теории гравитации, чтобы действительно «излечить» эту болезнь математики.

Особый интерес представляет возможность существования сингулярностей конечного объема. Определение точных условий, приводящих к подобным образованиям, и их физическая интерпретация — задача, требующая не только более сложных вычислений, но и принципиально нового взгляда на топологию пространства-времени. Ограничения, связанные с использованием теории возмущений по производным, требуют разработки непертурбативных методов анализа.

В конечном счете, задача состоит не в том, чтобы усовершенствовать описание падения в бездну, а в том, чтобы понять, почему бездна существует. И, возможно, ответ лежит не в усложнении моделей, а в их радикальном упрощении. Иногда, чтобы увидеть лес, нужно перестать считать деревья.

Оригинал статьи: https://arxiv.org/pdf/2601.21658.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-30 21:24