Волны с переменной когерентностью: новые границы достижимого

Автор: Денис Аветисян

Исследование устанавливает универсальные пределы для наблюдаемых характеристик волн с различной степенью когерентности, основанные на анализе их спектра.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал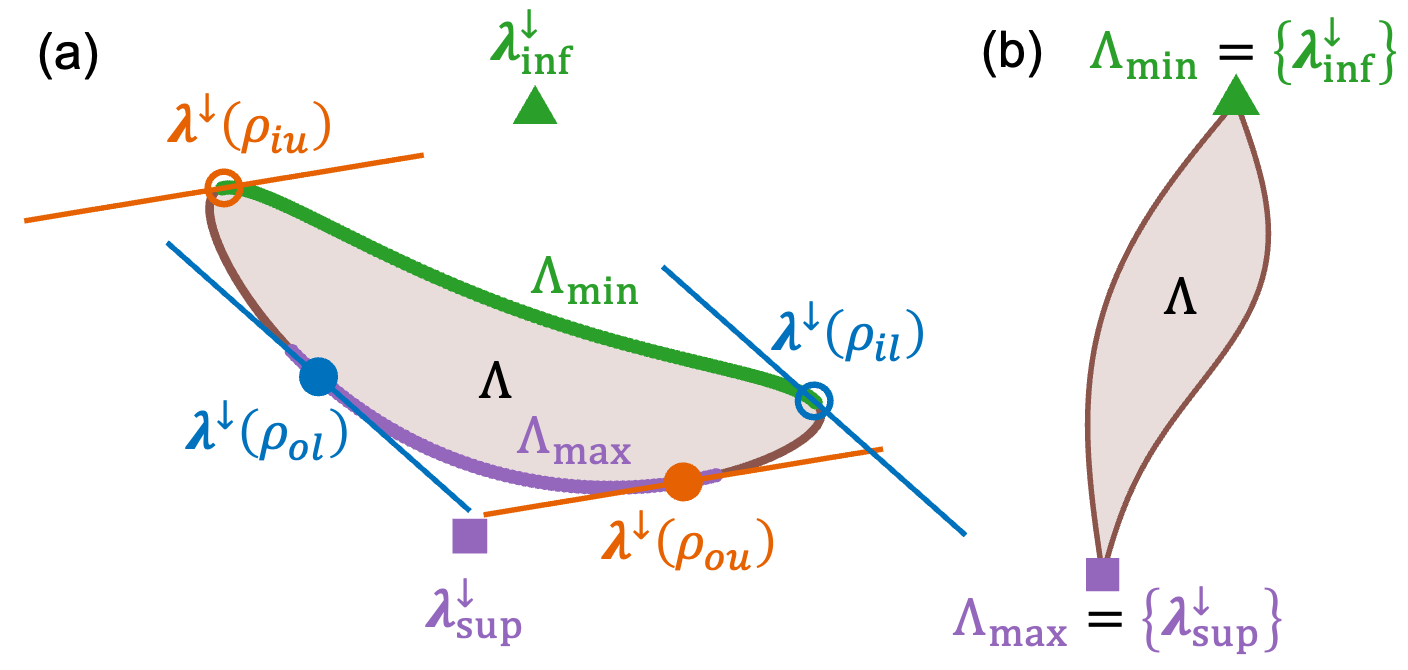

Компактное множество Λ когерентных спектров характеризуется наличием максимальных и минимальных элементов <span class="katex-eq" data-katex-display="false">\Lambda_{max}</span> и <span class="katex-eq" data-katex-display="false">\Lambda_{min}</span>, определяющих внешние и внутренние границы соответственно, причём предел <span class="katex-eq" data-katex-display="false">\lambda^{\downarrow}_{sup}</span> и нижняя грань <span class="katex-eq" data-katex-display="false">\lambda^{\downarrow}_{inf}</span> обычно выходят за пределы самого множества Λ, однако в особых случаях они могут совпадать с единственным максимумом и минимумом этого множества. — Компактное множество Λ когерентных спектров характеризуется наличием максимальных и минимальных элементов $\Lambda_{max}$ и $\Lambda_{min}$ , определяющих внешние и внутренние границы соответственно, причём предел $\lambda^{\downarrow}_{sup}$ и нижняя грань $\lambda^{\downarrow}_{inf}$ обычно выходят за пределы самого множества Λ, однако в особых случаях они могут совпадать с единственным максимумом и минимумом этого множества.

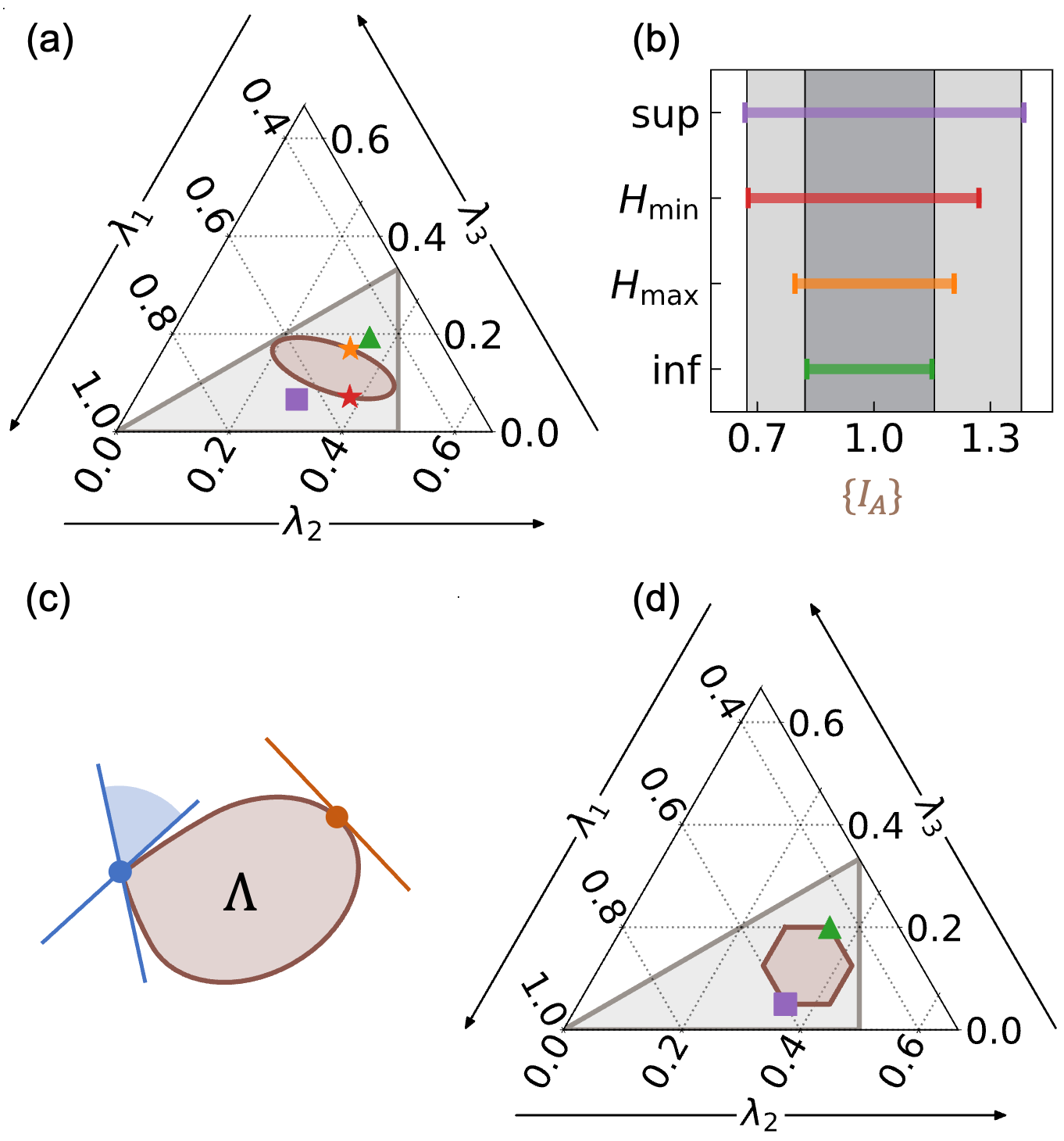
Оптимальные границы определяются супремумом и инфимумом множества когерентных значений, а не только минимальным и максимальным.

Несмотря на широкое использование характеристик когерентности для описания волновых процессов, установление универсальных границ достижимых наблюдаемых величин оставалось сложной задачей. В работе «Optimal universal bounds for waves with varied coherence based on supremum and infimum coherence spectra» разработана теория мажоризации, позволяющая определить оптимальные границы для наблюдаемых величин волн с переменной когерентностью. Показано, что эти границы определяются не максимальным и минимальным значениями спектра когерентности, а его супремумом и инфимумом, лежащими за пределами самого множества. Каким образом предложенный подход может быть расширен для анализа более сложных волновых систем и нелинейных эффектов?

Когерентность как Граница Познания: Пределы Волновых Систем

Понимание поведения волн неразрывно связано с характеристикой их когерентности, однако традиционные подходы оказываются недостаточно эффективными при анализе сложных систем. Классические методы, зачастую основанные на упрощенных моделях, не способны адекватно описать взаимодействия в средах с высокой степенью неоднородности или при наличии множественных источников волн. Это приводит к неточностям в прогнозировании распространения волн, особенно в задачах, связанных с оптикой, акустикой и сейсмологией. Современные исследования направлены на разработку новых методов, учитывающих пространственно-временные характеристики когерентности и позволяющих более точно моделировать волновые процессы в сложных условиях, используя, например, корреляционные функции и спектральный анализ для количественной оценки степени когерентности в различных точках пространства.

Распространение волн, описываемое волновым фронтом, является основополагающим принципом в физике, однако полное предсказание отклика системы требует детального понимания ее когерентности. Волновая функция описывает эволюцию волны во времени и пространстве, но эта эволюция существенно зависит от степени корреляции между различными точками волнового фронта. Недостаточное знание когерентных свойств приводит к неточностям в моделировании и прогнозировании, особенно в сложных системах, где интерференция и дифракция играют важную роль. Таким образом, для точного анализа и предсказания поведения волн необходимо не только учитывать геометрию волнового фронта, но и тщательно характеризовать когерентность источника и среды распространения, включая такие параметры, как временная и пространственная когерентность, а также поляризационные свойства $E(r,t)$ .

Для точного предсказания отклика сложных систем на волны требуется не просто знание когерентности, но и четкое определение границ достижимых ответов, обусловленных её свойствами. Разрабатывается строгая математическая структура, позволяющая установить, какие типы волн и с какими характеристиками могут быть успешно сформированы и направлены, учитывая ограничения, накладываемые когерентностью источника. Данный подход позволяет перейти от описания “что возможно” к определению “что достижимо в данных условиях”, что критически важно для проектирования оптических систем, акустических устройств и других технологий, использующих волновые явления. $\Delta x \Delta p \ge \frac{\hbar}{2}$ — подобное фундаментальное ограничение, известное из квантовой механики, находит аналоги в области когерентности, определяя компромисс между точностью определения параметров волны и её пространственной локализацией.

Исследование переноса частично когерентных волн в диффузионных волноводах показывает, что при увеличении числа мод (от n=2 до n=3) порядок мажоризации становится частичным, а диапазоны интенсивностей перестают вкладываться друг в друга, при этом оптимальные универсальные границы для всех измерений определяются супремумом и инфимумом, выходящими за пределы исходного множества.

Спектр Когерентности: Ключ к Ограничениям и Возможностям

Когерентоспектр представляет собой полное описание когерентности волны, предоставляя информацию о ее фазовой и амплитудной стабильности во времени и пространстве. В отличие от традиционных методов анализа когерентности, которые часто ограничиваются рассмотрением корреляционных функций или степеней когерентности, когерентоспектр оперирует с полным спектром когерентных свойств. Он позволяет определить степень корреляции между различными частотными компонентами волны и, следовательно, является основой для последующего анализа ограничений на наблюдаемые отклики и построения теорий, основанных на принципах мажоризации. $S(\omega)$ — типичное обозначение когерентоспектра в частотной области, где ω представляет собой частоту.

В рамках анализа когерентных сигналов, границы ‘ВнутренняяГраница’ (InnerBound) и ‘ВнешняяГраница’ (OuterBound) определяются как минимально и максимально достижимые значения отклика, определяемые спектром когерентности. $InnerBound$ представляет собой инфимум возможных значений отклика, а $OuterBound$ — супремум. Эти границы не являются абсолютными пределами, но представляют собой теоретические ограничения, накладываемые структурой когерентности сигнала, и служат основой для разработки теорий мажоризации, позволяющих оценивать и ограничивать наблюдаемые диапазоны значений отклика.

Пределы отклика, определяемые спектром когерентности, математически формализуются посредством понятий инфимума (наименьшей верхней границы) и супремума (наибольшей нижней границы). Инфимум определяет минимально возможное значение отклика для заданной частоты, в то время как супремум определяет максимальное. Эти математические конструкции позволяют построить теорию мажоризации, которая предоставляет строгие границы для наблюдаемых диапазонов отклика. Формально, для функции отклика $R(\omega)$ , инфимум $inf R(\omega)$ и супремум $sup R(\omega)$ задают нижнюю и верхнюю границы соответственно, обеспечивая точное определение пределов, в которых может изменяться наблюдаемый сигнал.

Спектры когерентности, достигающие внешних (заполненные круги) и внутренних (пустые круги) границ для измерений <span class="katex-eq" data-katex-display="false">IAI_A</span> и <span class="katex-eq" data-katex-display="false">IBI_B</span> при <span class="katex-eq" data-katex-display="false">n=3</span> эллиптического диска из рис. 3(a), являются элементами <span class="katex-eq" data-katex-display="false">\Lambda_{max}</span> (фиолетовый) и <span class="katex-eq" data-katex-display="false">\Lambda_{min}</span> (зеленый), что подтверждает, что максимальные и минимальные элементы достигают точных внешних и внутренних границ. — Спектры когерентности, достигающие внешних (заполненные круги) и внутренних (пустые круги) границ для измерений $IAI_A$ и $IBI_B$ при $n=3$ эллиптического диска из рис. 3(a), являются элементами $\Lambda_{max}$ (фиолетовый) и $\Lambda_{min}$ (зеленый), что подтверждает, что максимальные и минимальные элементы достигают точных внешних и внутренних границ.

Порядок Когерентности: Иерархия и Ограничения

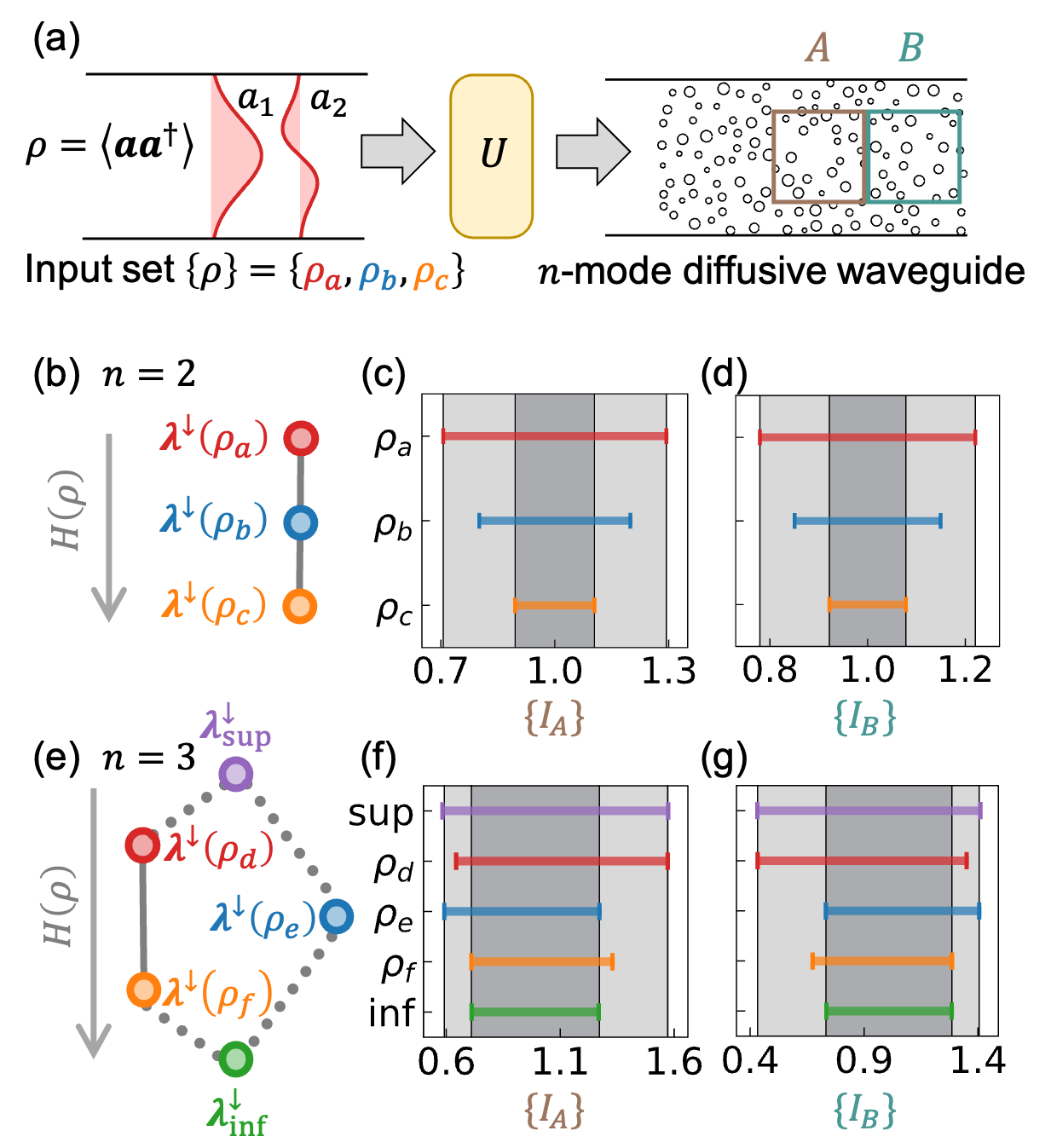
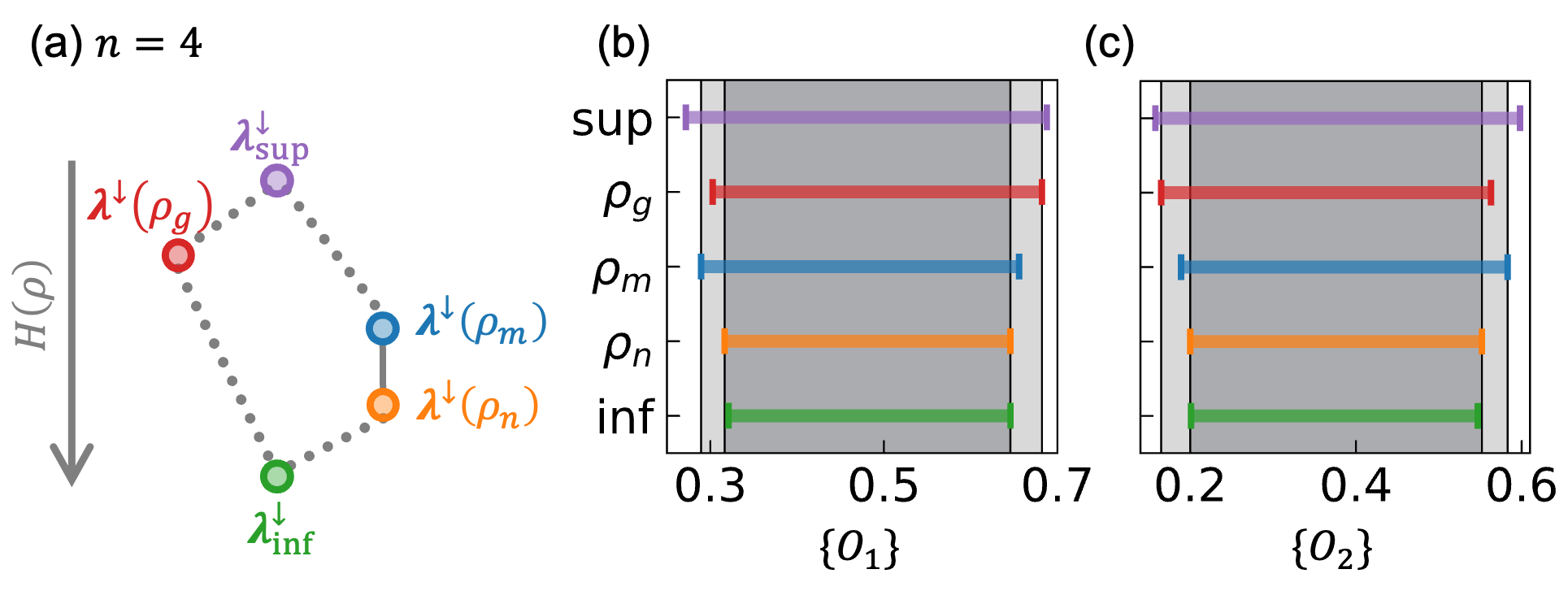
Метод ‘MajorizationOrder’ предоставляет способ сравнения спектров когерентности, выявляя иерархию достижимых откликов. Сравнение осуществляется на основе принципа мажоризации, позволяющего установить частичный порядок между различными состояниями когерентности. Более «мажоризованное» состояние представляет собой более упорядоченную и, следовательно, более ограниченную форму отклика, в то время как «миноризованное» состояние обладает большей степенью свободы. Этот порядок позволяет определить, какие отклики являются физически реализуемыми для данного спектра когерентности, и установить границы для возможных наблюдаемых результатов. Таким образом, ‘MajorizationOrder’ не просто сравнивает спектры, но и раскрывает взаимосвязь между когерентностью и пространством достижимых откликов.

Визуализация порядка когерентности с помощью диаграммы Хассе (Hasse Diagram) предоставляет наглядное представление о взаимосвязи между различными спектрами когерентности и соответствующими им возможностями отклика. В данной структуре каждый узел представляет собой определенный спектр когерентности, а направленные ребра указывают на доминирование одного спектра над другим, определяемое частичным порядком. Диаграмма позволяет визуально определить, какие состояния когерентности являются достижимыми из других, и как изменения в когерентности влияют на диапазон возможных откликов системы. Использование диаграммы Хассе упрощает анализ и понимание иерархии когерентных состояний, облегчая выявление оптимальных стратегий управления когерентностью для достижения желаемых результатов.

Применение операции ‘LinearCombination’ к спектрам когерентности позволяет конструировать более сложные состояния из более простых, сохраняя при этом иерархический порядок, определяемый ‘MajorizationOrder’. Данный подход предполагает, что любое состояние, полученное в результате линейной комбинации, будет подчиняться тем же ограничениям, что и исходные спектры когерентности, участвующие в комбинации. Использование ‘LinearCombination’ обеспечивает возможность систематического построения сложных состояний, удовлетворяющих определенным критериям когерентности, и позволяет исследовать пространство допустимых состояний в рамках установленного порядка мажоризации. Результатом является возможность предсказуемого и контролируемого построения сложных квантовых состояний из базовых, при сохранении их когерентных свойств.

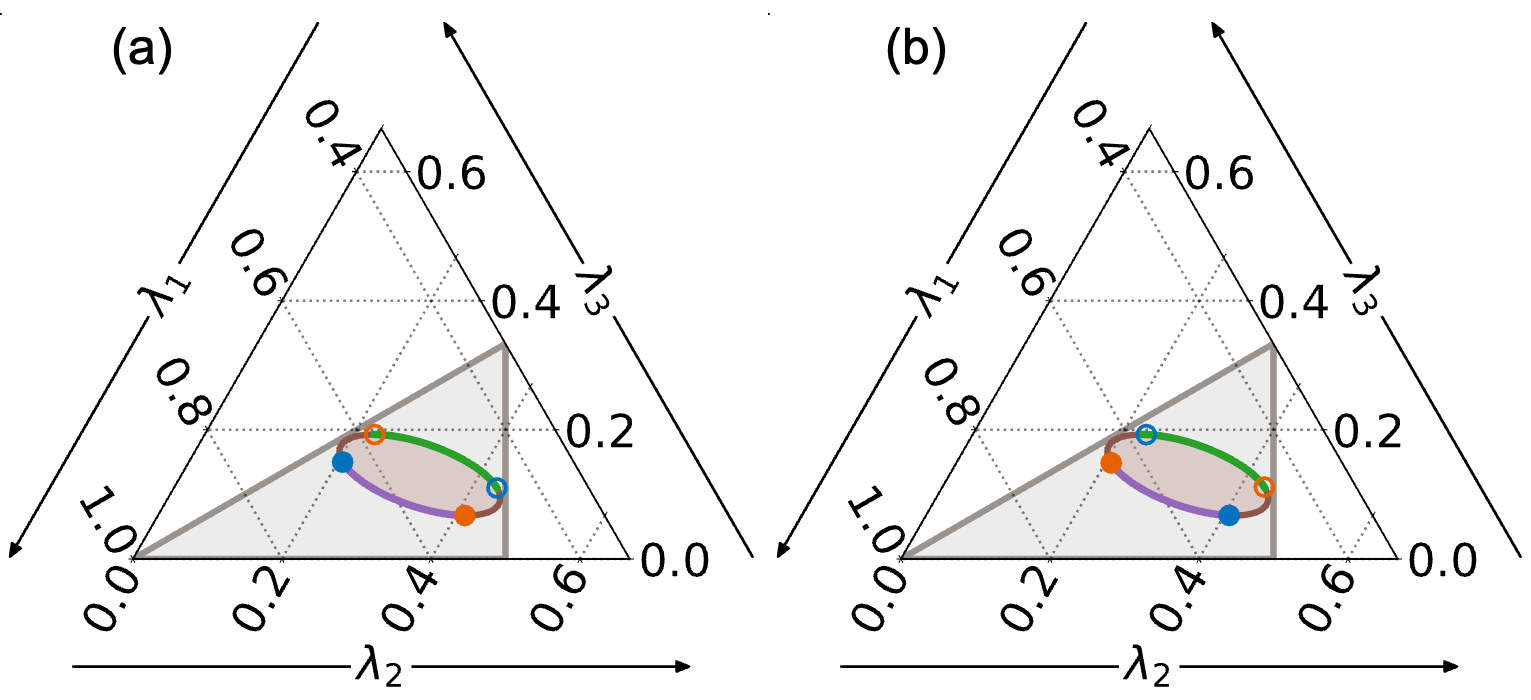
Вычисление супремума и инфимума в рамках данного метода демонстрирует скорость сходимости, пропорциональную $O(N^{-2})$ , где N — количество вершин многоугольника. Это означает, что с увеличением числа вершин, точность аппроксимации супремума и инфимума возрастает обратно пропорционально квадрату количества вершин. Практически, это указывает на квадратичную сходимость алгоритма, требующую увеличения вычислительных ресурсов для достижения более высокой точности при увеличении детализации представления спектра когерентности.

Анализ когерентных спектров <span class="katex-eq" data-katex-display="false">m{\lambda}^{\downarrow}(\rho\_{g})</span>, <span class="katex-eq" data-katex-display="false">m{\lambda}^{\downarrow}(\rho\_{m})</span> и <span class="katex-eq" data-katex-display="false">m{\lambda}^{\downarrow}(\rho\_{n})</span> посредством диаграммы Хассе демонстрирует отношения мажоризации и связь с энтропией, а полученные границы достижимых значений операторов <span class="katex-eq" data-katex-display="false">O_1</span> и <span class="katex-eq" data-katex-display="false">O_2</span> подтверждают, что границы супремума и инфимума содержат все возможные значения для состояний g, m и n. — Анализ когерентных спектров $m{\lambda}^{\downarrow}(\rho\_{g})$ , $m{\lambda}^{\downarrow}(\rho\_{m})$ и $m{\lambda}^{\downarrow}(\rho\_{n})$ посредством диаграммы Хассе демонстрирует отношения мажоризации и связь с энтропией, а полученные границы достижимых значений операторов $O_1$ и $O_2$ подтверждают, что границы супремума и инфимума содержат все возможные значения для состояний g, m и n.

Чувствительность Границ: От Гладкой Стабильности к Сингулярным Точкам

Гладкая граница в контексте исследуемой системы указывает на её устойчивость к незначительным изменениям в когерентности. Это означает, что даже при небольших колебаниях параметров, определяющих связность системы, наблюдаемые реакции остаются предсказуемыми и не претерпевают резких трансформаций. Подобная характеристика свидетельствует о способности системы эффективно справляться с шумами и возмущениями, сохраняя функциональность и надежность. Исследование гладких границ позволяет понять, какие механизмы обеспечивают стабильность системы и как её можно оптимизировать для работы в условиях неопределенности. В отличие от сингулярных точек, где малейшее отклонение в когерентности приводит к кардинальным изменениям, гладкая граница гарантирует предсказуемость и контролируемость поведения системы.

Особая граница, обозначенная как “Сингулярная Граница”, демонстрирует крайне высокую чувствительность системы к малейшим изменениям в когерентности. В отличие от устойчивых границ, даже незначительные колебания в параметрах когерентности приводят к существенным изменениям в наблюдаемых откликах. Это означает, что система, находящаяся вблизи такой границы, может быстро и непредсказуемо переключаться между различными состояниями. Изучение этих сингулярных точек позволяет понять, какие факторы определяют стабильность системы и предсказать её поведение в условиях неопределенности, а также выявить потенциальные точки бифуркации, где небольшие воздействия могут привести к масштабным последствиям.

Определение границ системы как «гладких» или «сингулярных» предоставляет важные сведения о её стабильности и предсказуемости. Гладкая граница указывает на устойчивость — незначительные изменения в когерентности не приводят к резким изменениям в наблюдаемых ответах системы. В отличие от этого, сингулярная точка границы демонстрирует крайнюю чувствительность: даже небольшие колебания в когерентности могут спровоцировать существенные изменения в поведении системы. Таким образом, классификация границ позволяет оценить, насколько надёжно система сохраняет свои функции при незначительных внешних воздействиях, и предсказать её реакцию на различные условия, что критически важно для проектирования устойчивых и предсказуемых систем.

Для более глубокого понимания чувствительности границ, обусловленной когерентностью, представляется полезным рассмотрение энтропии как меры беспорядка в спектре когерентности. Высокая энтропия указывает на значительное разнообразие в когерентных состояниях, что, в свою очередь, может указывать на повышенную чувствительность границы к незначительным изменениям. Иными словами, система с высокой энтропией в спектре когерентности будет демонстрировать более выраженную реакцию на малейшие флуктуации, в то время как низкая энтропия предполагает большую устойчивость и предсказуемость поведения. Таким образом, анализ энтропии позволяет количественно оценить степень «беспорядочности» когерентных состояний и, следовательно, более точно охарактеризовать чувствительность границ к изменениям в системе.

Установлено, что размерность нормального конуса в точках супремума и инфимума всегда составляет n-1, что представляет собой фундаментальное геометрическое свойство граничных точек. Данный результат, полученный в ходе строгих математических доказательств, указывает на то, что в этих критических точках пространство решений ограничено гиперплоскостью, размерность которой на единицу меньше, чем размерность исходного пространства. Это свойство имеет важные последствия для понимания устойчивости и предсказуемости систем, поскольку указывает на то, что небольшие изменения в условиях могут привести к существенным изменениям в ответах системы, но эти изменения ограничены определенной гиперплоскостью. Исследование размерности нормального конуса позволяет более точно характеризовать границы стабильности и прогнозировать поведение систем вблизи этих границ, открывая возможности для разработки более надежных и эффективных алгоритмов управления и оптимизации.

Анализ компактного множества Λ в пространстве <span class="katex-eq" data-katex-display="false">\Delta_n^\downarrow</span> показывает, что его супремум и инфимум достигаются в сингулярных точках или за пределами множества, при этом границы выпуклого множества определяют диапазон допустимых значений <span class="katex-eq" data-katex-display="false">I_A</span> и <span class="katex-eq" data-katex-display="false">I_B</span>, как показано на примере эллиптического диска и гексагональной области. — Анализ компактного множества Λ в пространстве $\Delta_n^\downarrow$ показывает, что его супремум и инфимум достигаются в сингулярных точках или за пределами множества, при этом границы выпуклого множества определяют диапазон допустимых значений $I_A$ и $I_B$ , как показано на примере эллиптического диска и гексагональной области.

Исследование, представленное в данной работе, демонстрирует стремление к выявлению предельных возможностей волновых процессов, определяемых не только минимальным, но и супремумом и инфимумом когерентности. Этот подход к определению границ достижимых наблюдаемых величин перекликается с философией Петра Капицы: «Не бойтесь нарушать правила, если хотите понять систему». Ведь именно через проверку границ, через исследование того, что происходит при отклонении от установленных норм, открываются новые горизонты понимания. В данном случае, исследование когерентности показывает, что истинные пределы определяются не столько консервативными оценками, сколько полным спектром возможных состояний, что соответствует духу реверс-инжиниринга реальности, который так ценил Капица.

Что дальше?

Представленная работа, по сути, лишь аккуратно выстроенный мост. Мост, соединяющий формальный математический аппарат теории мажоризации с весьма упрямой реальностью волновой оптики. Утверждается, что супремум и инфимум когерентного спектра определяют границы достижимого. Но что, если сама концепция «когерентности», как мы её понимаем, — это лишь удобное приближение, а истинная природа волновых явлений гораздо сложнее? Не стоит забывать, что любая «оптимальность» — это лишь локальное, временное решение в рамках заданных ограничений.

Очевидным следующим шагом представляется расширение полученных результатов на неклассические волновые функции, например, на состояния, описываемые неэрмитовыми операторами. Ведь если границы достижимого определяются супремумом и инфимумом, то нарушение стандартных предпосылок о симметрии системы может привести к неожиданным и, возможно, крайне полезным эффектам. Это как взлом системы: найдя брешь, можно получить доступ к новым возможностям.

Впрочем, самое интересное, вероятно, лежит в области применения. Поиск волновых функций, оптимальных по заданным критериям, — задача, требующая значительных вычислительных ресурсов. Но если удастся разработать эффективные алгоритмы, можно будет создавать оптические устройства с беспрецедентными характеристиками. И тогда «баг» в системе, обнаруженный благодаря исследованию границ достижимого, станет не ошибкой, а ключом к новому уровню понимания.

Оригинал статьи: https://arxiv.org/pdf/2601.10665.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-19 00:38