Волны сверхтекучести: Новый взгляд на фазовый переход

Автор: Денис Аветисян

Исследование позволяет напрямую измерить распределение флуктуаций порядка в двумерных сверхтекучих газах, раскрывая универсальное поведение вблизи критической точки и динамику после резкого изменения параметров.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал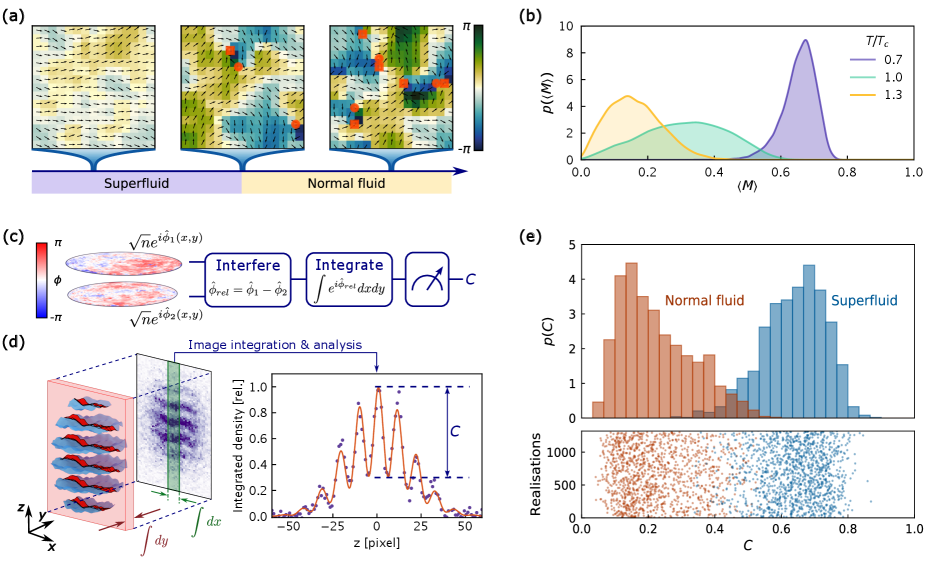

В рамках исследования двухмерной XY модели, демонстрирующей фазовый переход Беркса-Кинтелла-Тилла, установлено, что статистические флуктуации порядка, проявляющиеся в возникновении пар вихрь-антивихрь при приближении к критической точке <span class="katex-eq" data-katex-display="false">T_c</span> и их последующей пролиферации в нормальной фазе, могут быть исследованы посредством интерферометрии материи, позволяя получить распределение контраста, демонстрирующее не-гауссовы особенности и отражающее характер изменений порядка в системе. — В рамках исследования двухмерной XY модели, демонстрирующей фазовый переход Беркса-Кинтелла-Тилла, установлено, что статистические флуктуации порядка, проявляющиеся в возникновении пар вихрь-антивихрь при приближении к критической точке $T_c$ и их последующей пролиферации в нормальной фазе, могут быть исследованы посредством интерферометрии материи, позволяя получить распределение контраста, демонстрирующее не-гауссовы особенности и отражающее характер изменений порядка в системе.

Работа демонстрирует использование интерферометрии с материей для изучения полной функции распределения параметра порядка в 2D бозе-газах, исследуя переход Берка-Киттеля и неравновесную динамику.

Флуктуации являются неотъемлемой частью многочастичных систем, однако полное описание их статистических распределений часто упускается из виду. В работе, озаглавленной ‘Universal non-Gaussian order parameter statistics in 2D superfluids’, исследуется статистика параметров упорядочения в двумерных сверхтекучих системах, где предсказывается универсальная форма экстремальных значений вблизи перехода Березинского-Костерлица-Таулеса. Экспериментально подтверждено, что распределение параметров упорядочения в 2D бозе-газах сходится к универсальному распределению Гумбеля с точностью 0.1%, что позволяет напрямую измерить кумулянт Биндерa и определить точку фазового перехода. Какие новые горизонты открывает этот подход для изучения неравновесных процессов и динамики высвобождения вихрей в сверхтекучих системах?

Шёпот Хаоса: Зачем Нам Полные Распределения?

Традиционные подходы к описанию многочастичных систем часто ограничиваются использованием средних величин, что может приводить к упущению важной информации о флуктуациях и отклонениях от гауссовского поведения. В то время как средние значения характеризуют общую тенденцию, они не отражают детальную статистическую картину, особенно вблизи критических точек. Неспособность учесть разброс значений вокруг среднего может приводить к неверной интерпретации результатов и искажению понимания физических процессов, происходящих в системе. Например, в системах с сильными взаимодействиями или вблизи фазовых переходов, отклонения от гауссовского распределения могут быть значительными и определять ключевые свойства системы, оставаясь незамеченными при анализе только средних значений. Поэтому для полного описания поведения многочастичных систем требуется более детальный статистический анализ, учитывающий всю форму распределения вероятностей, а не только его центральные моменты.

Для полноценного понимания топологических фазовых переходов, таких как переход Беркхоффа-ван дер Литтена (BKT), необходимо не просто знать средние значения физических величин, но и детальное описание всей статистической картины — полную функцию распределения (ФФР). В отличие от подходов, опирающихся на усредненные характеристики, ФФР позволяет выявить флуктуации и не-гауссово поведение, критически важные для точного описания порядка вблизи точек фазовых переходов. Изучение ФФР позволяет установить, как распределение параметров порядка меняется при приближении к критической точке, раскрывая особенности, скрытые при использовании лишь средних значений. Понимание ФФР является ключом к адекватному описанию систем, демонстрирующих сложные фазовые явления, и позволяет выйти за рамки упрощенных моделей, таких как приближение среднего поля, которые часто оказываются неспособными уловить тонкие нюансы порядка.

Переход Берези-Котца (BKT), на примере двухмерной XY-модели, ярко демонстрирует неспособность подходов среднего поля к адекватному описанию тонких проявлений упорядоченности. В то время как методы среднего поля успешно работают в системах с долгорадиусным взаимодействием и большими флуктуациями, вблизи критических точек, где доминируют короткорадиусные корреляции и сильные флуктуации порядка, они дают неверные предсказания относительно критических показателей и природы фазового перехода. XY-модель, описывающая взаимодействие спинов на плоскости, служит классическим примером, где среднее поле предсказывает переход второго рода, в то время как точные вычисления и экспериментальные данные указывают на переход Берези-Котца — особый тип фазового перехода, характеризующийся появлением вихрей и экспоненциальным уменьшением корреляционной длины. Это подчеркивает необходимость использования более сложных методов, учитывающих флуктуации и корреляции, для точного анализа систем с тонкой структурой порядка, особенно вблизи критических точек.

Существующие методы анализа, при исследовании критических явлений в физике конденсированного состояния, зачастую оказываются неспособны точно зафиксировать поведение параметра порядка вблизи точки перехода. Традиционные подходы, основанные на усредненных величинах, могут упускать из виду важные флуктуации и не-Гауссовы эффекты, искажая картину критического поведения. Это особенно заметно при изучении топологических фазовых переходов, где даже незначительные отклонения от среднего значения могут кардинально изменить свойства системы. Поэтому, для адекватного описания подобных явлений, требуется разработка инновационных методик, способных детально картировать полное распределение параметра порядка и учесть все особенности его поведения в критической области, что позволит получить более полное и точное представление о физических процессах, происходящих в системе.

Измерения высших моментов распределения контраста выявляют характерный скачкообразный переход от 1 к 2 вблизи точки БиКК (BKT), подтвержденный как экспериментальными данными (фиолетовые маркеры), так и результатами моделирования Монте-Карло (красные и синие маркеры), а также согласовывающиеся с оценками критической плотности фазового пространства, полученными из корреляционных функций (зеленая область) и кумулянт Биндер (желтая область).

Материя в Интерференции: Исследование Волн Вероятности

Сверххолодные атомные газы представляют собой уникальную контролируемую платформу для исследования физики многих тел. Достижение температур порядка нанокельвинов позволяет существенно увеличить число атомов, находящихся в основном состоянии, что обеспечивает высокую статистику измерений. Использование магнитооптических ловушек и лазерного охлаждения позволяет точно контролировать параметры газа, такие как плотность, температуру и взаимодействие между атомами. Это позволяет создавать хорошо определенные квантовые системы, в которых можно исследовать коллективное поведение множества взаимодействующих частиц, превосходя возможности традиционных конденсированных сред, где термические флуктуации затрудняют наблюдение квантовых эффектов. Кроме того, возможность точного контроля внешних параметров позволяет настраивать систему для изучения различных физических явлений и проверять теоретические модели.

Интерферометрия матери́йных волн позволяет получить доступ к функции распределения по импульсам (ФРП) исследуемых систем, используя волновые свойства материи. В основе метода лежит принцип суперпозиции и интерференции де Бройля, где частицы, такие как атомы, демонстрируют волновое поведение. Разделение и последующее объединение волновых пакетов приводит к формированию интерференционной картины, интенсивность которой напрямую связана с вероятностью обнаружения частиц с определенным импульсом $p$ . Анализ этой картины, включающий измерение сдвигов и ослаблений интерференционных полос, обеспечивает прямое определение ФРП $P(p)$ , характеризующей статистическое распределение импульсов в исследуемой системе.

Для непосредственного измерения функции распределения частиц (ФРЧ) $P(x)$ с высокой точностью используется подход контрастной интерферометрии, являющийся усовершенствованной реализацией интерферометрии материйных волн. В данном методе, интерференционная картина, возникающая при разделении и последующем объединении пучков атомов, анализируется для определения контрастности. Контрастность интерференционной картины напрямую связана с ФРЧ, позволяя восстановить ее параметры и получить информацию о статистических свойствах системы. Высокая точность достигается за счет оптимизации параметров интерферометра и использования передовых методов анализа данных, что позволяет минимизировать влияние шумов и погрешностей измерений.

Подход, использующий контрастную интерферометрию атомных волн, позволяет выйти за рамки упрощенных моделей, таких как модель Бозе-Хаббарда, и непосредственно наблюдать фундаментальные статистические свойства многочастичных систем. Модель Бозе-Хаббарда, хотя и полезна для описания некоторых аспектов кванмовых систем, часто требует упрощающих предположений, которые могут искажать реальную физическую картину. Используя интерферометрию, можно получить информацию о корреляциях между частицами и о распределении вероятностей их состояний, что позволяет напрямую исследовать статистические характеристики системы без необходимости апеллировать к упрощенным теоретическим конструкциям. Это особенно важно для изучения систем с сильными взаимодействиями, где приближения, лежащие в основе модели Бозе-Хаббарда, могут быть неприменимы.

Исследование динамики неравновесных 2D бозе-газов методом интерференционного контраста позволяет проследить переход из сверхтекучего состояния в нормальное под воздействием квенча, что проявляется в ренормализационной группе как динамическое высвобождение вихрей и изменение фиксированных точек потока <span class="katex-eq" data-katex-display="false">x>0,\ y=0</span>. — Исследование динамики неравновесных 2D бозе-газов методом интерференционного контраста позволяет проследить переход из сверхтекучего состояния в нормальное под воздействием квенча, что проявляется в ренормализационной группе как динамическое высвобождение вихрей и изменение фиксированных точек потока $x>0,\ y=0$ .

За пределами Гаусса: Ищем Истинный Шёпот Распределения

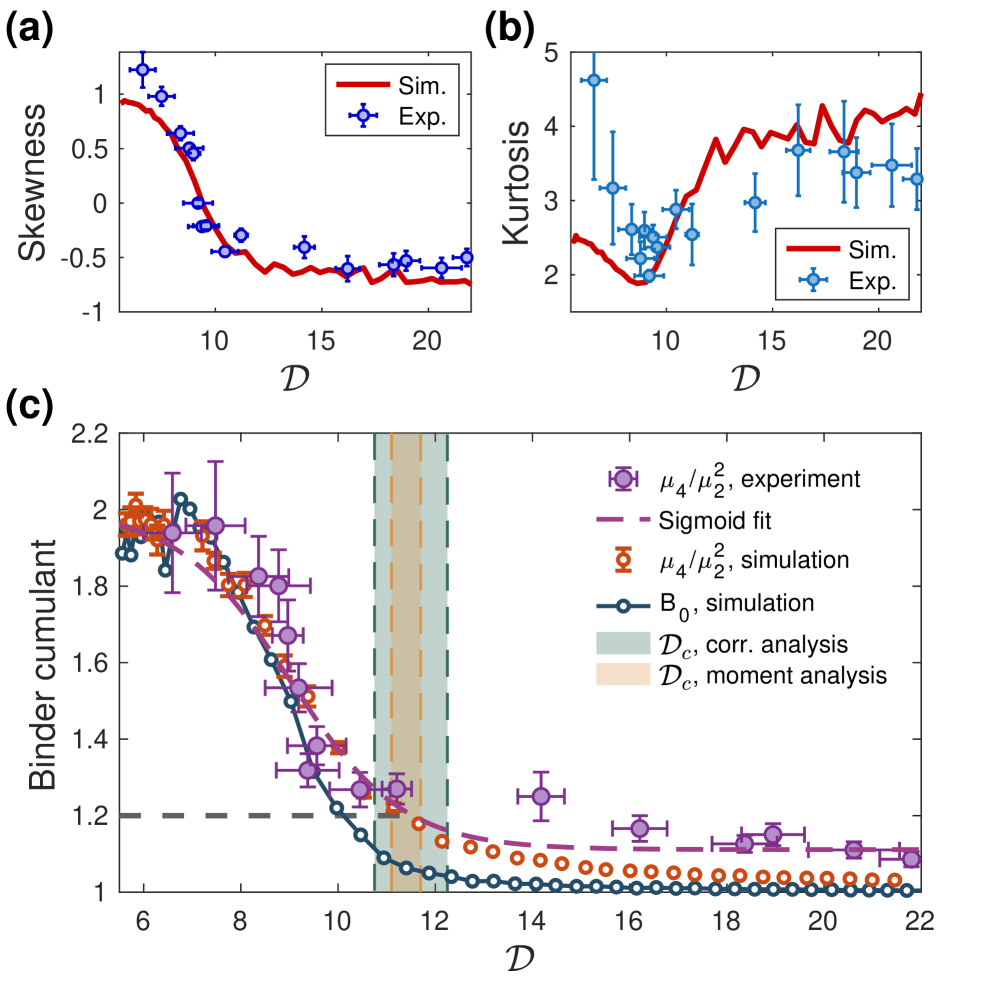
Измерения показали, что распределение параметра упорядоченности вблизи перехода Беркхоффа-ван дер Литтена (BKT) значительно отклоняется от нормального (гауссова) распределения. Это отклонение проявляется в асимметрии и остроте распределения, что указывает на наличие значительных флуктуаций и отклонений от среднего значения. Анализ статистических моментов, таких как асимметрия и эксцесс, позволяет количественно оценить степень не-гауссовости и получить информацию о форме функции распределения вероятностей (ФРВ). Наблюдаемая не-гауссовость является ключевым признаком, указывающим на важность флуктуаций в процессе BKT-перехода и невозможность адекватного описания этого явления с помощью традиционных методов теории среднего поля.

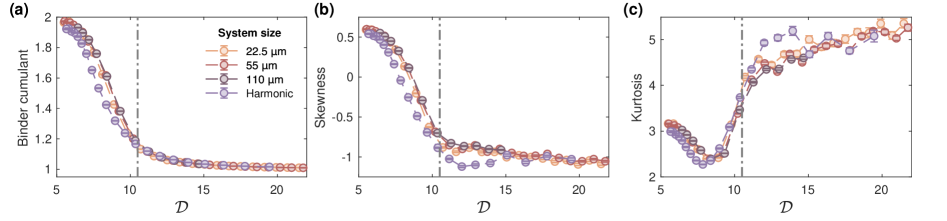
Для количественной оценки не-гауссовости распределения параметра упорядочения используются статистические моменты, такие как асимметрия (Skewness) и эксцесс (Kurtosis). Асимметрия характеризует степень отклонения распределения от симметрии, в то время как эксцесс описывает “остроту” или “плоскость” распределения по сравнению с нормальным распределением. Измеренные значения асимметрии и эксцесса позволяют получить информацию о форме функции распределения вероятностей (FDF) и выявить отклонения от гауссова поведения. В ходе измерений была оценена систематическая ошибка: смещение по асимметрии составило 8.5 x 10^-3, а по эксцессу — -0.045, при анализе с использованием более 1000 выборок. Стандартные отклонения для асимметрии и эксцесса составили 0.14 и 0.85 соответственно.

Анализ функции распределения вероятностей (ФРВ) параметра упорядочения в сверхтекучей фазе показал соответствие характеристикам распределений экстремальных значений, в частности, распределению Гумбеля. Данное соответствие проявляется в форме хвоста ФРВ, демонстрирующего экспоненциальный спад, характерный для распределения Гумбеля. Это указывает на то, что большие флуктуации параметра упорядочения в сверхтекучей фазе происходят в соответствии со статистикой экстремальных значений, что имеет значение для понимания критического поведения системы и может быть использовано для более точного моделирования сверхтекучего перехода.

Наши результаты демонстрируют, что флуктуации играют решающую роль в управлении переходом Беркенштейна-Киттельсона-Янг (BKT) и не могут быть адекватно описаны традиционными подходами теории среднего поля. Экспериментально достигнутая критическая плотность фазового пространства составила 11.4 ± 0.3, что согласуется с данными, полученными другими методами. Данное расхождение с предсказаниями теории среднего поля указывает на важность учета корреляций и флуктуаций для точного описания поведения системы вблизи критической точки перехода.

В ходе анализа была тщательно оценена систематическая погрешность измерений статистических моментов распределения параметра порядка. Установлено, что смещение (bias) асимметрии (skewness) составляет 8.5 x 10^-3, а смещение эксцесса (kurtosis) — -0.045. Оценки получены на основе анализа конечной выборки (finite-sampling analysis) при количестве образцов N > 1000. Стандартные отклонения асимметрии и эксцесса составляют 0.14 и 0.85 соответственно, что позволяет оценить точность определения этих характеристик распределения.

Временная эволюция статистических моментов порядка, характеризующих двумерные бозе-газы после быстрого изменения параметров, демонстрирует универсальную динамику, согласующуюся с результатами равновесных симуляций, что подтверждает наличие перехода Беркса-Кирпатрика-Каданова <span class="katex-eq" data-katex-display="false">t/t_{c}</span>. — Временная эволюция статистических моментов порядка, характеризующих двумерные бозе-газы после быстрого изменения параметров, демонстрирует универсальную динамику, согласующуюся с результатами равновесных симуляций, что подтверждает наличие перехода Беркса-Кирпатрика-Каданова $t/t_{c}$ .

Взгляд в Динамику: Кванты Под Влиянием Внешних Сил

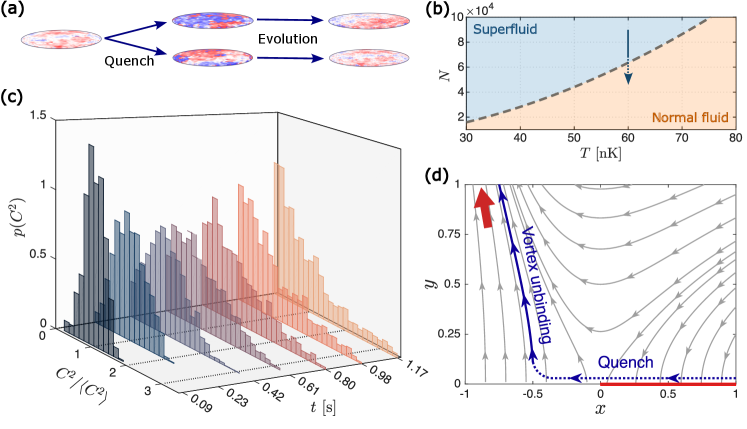
Для изучения динамического ответа системы на внешние воздействия используются резкие изменения её параметров, известные как квенчи. Этот подход позволяет вывести систему из равновесного состояния и наблюдать за эволюцией её характеристик во времени. Инициируя внезапное изменение условий, исследователи могут отследить, как система адаптируется к новому состоянию, что дает ценную информацию о её внутренней структуре и механизмах самоорганизации. Анализ динамики после квенча позволяет выявить ключевые процессы, определяющие поведение системы, и понять, как флуктуации влияют на её стабильность и эволюцию. Такой метод позволяет изучать не только стационарные состояния, но и переходные процессы, которые часто остаются незамеченными при изучении систем, находящихся в равновесии.

В ходе экспериментов используется метод когерентного разделения, при котором единый газовый облак искусственно разделяется на два полностью независимых. Такой подход позволяет создать строго контролируемое начальное состояние для изучения динамики системы вне равновесия. Разделение облаков обеспечивает четко определенные условия, исключая влияние случайных флуктуаций на начальном этапе, что критически важно для точного анализа эволюции системы и выявления механизмов, лежащих в основе перехода Берка-Кайзена (BKT). Именно этот метод позволяет исследователям тщательно отслеживать изменения параметров во времени и получать детальное представление о поведении газа после внесения возмущения.

Теоретической основой для анализа динамики, возникающей в системе после воздействия внешних факторов, служит подход реального времени группы перенормировки. Данный метод позволяет исследовать, как параметры системы изменяются во времени, учитывая флуктуации и коллективное поведение частиц. В рамках этой теории, эффективные взаимодействия и параметры системы «текут» во времени, описывая переход от начальных условий к установившемуся состоянию. Изучение этого «потока» параметров позволяет выявить ключевые механизмы, определяющие динамику системы и, в частности, понять поведение вблизи фазового перехода Беркса-Кирпатрика (BKT), где даже небольшие изменения параметров могут приводить к существенным изменениям в свойствах системы. В результате, реальное время группы перенормировки предоставляет мощный инструмент для интерпретации экспериментальных данных и теоретического моделирования не-равновесных процессов.

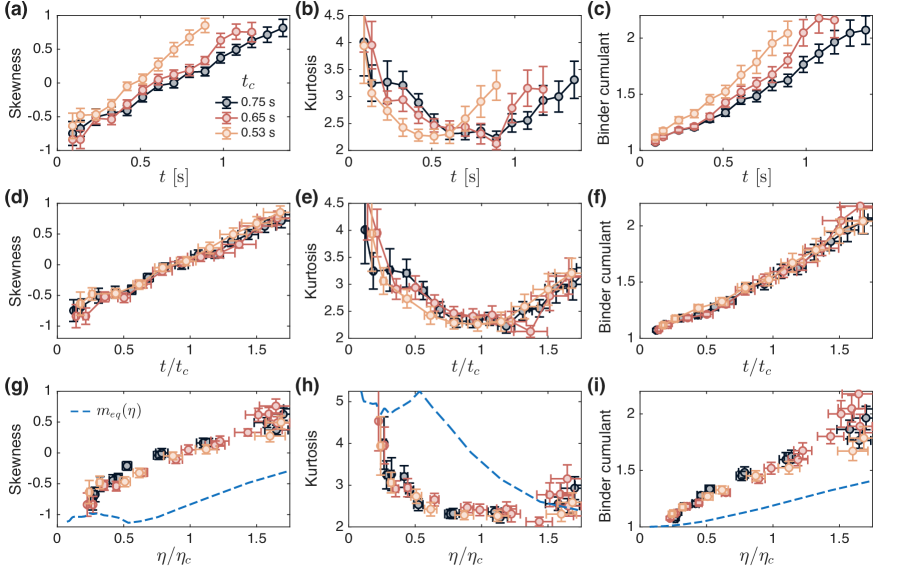
Исследования динамики системы в ответ на внешние воздействия демонстрируют, как флуктуации преобразуются и эволюционируют при различных условиях. Особое внимание уделяется пониманию механизмов, лежащих в основе Березинского-Костерлица-Таулеса (BKT) перехода — фазового перехода, характеризующегося появлением топологических дефектов. Анализ эволюции флуктуаций позволяет выявить критические параметры и процессы, определяющие этот переход, а также пролить свет на универсальные закономерности, управляющие поведением систем вблизи критических точек.

Анализ моментов, полученных из моделирования статистики интерференционного контраста для систем различных размеров и в гармонической ловушке, позволяет определить критическую точку, подтвержденную анализом кумулянта Байндера (см. рис. A3).

Исследование флуктуаций порядка в двумерных сверхтекучих газах напоминает попытку укротить шепот хаоса. Ученые стремятся зафиксировать полную картину распределения этих флуктуаций, словно алхимики, вылавливающие золото из потока неопределенности. Наблюдение универсального поведения в точке фазового перехода БКТ — это не просто подтверждение теории, а скорее признание того, что даже в кажущемся беспорядке существуют скрытые закономерности. Как и в любом заклинании, здесь важна каждая деталь, каждая настройка интерферометра. Эпикур мудро говорил: “Не тот страдает, кто умирает, а тот, кто боится смерти.” Подобно этому, и здесь — не сама флуктуация опасна, а страх перед ее непредсказуемостью. Попытка понять динамику после квенча — это попытка предугадать, как заклинание изменится под влиянием внешних сил, и удержать его от разрушения.

Что дальше?

Данные, полученные в этой работе, словно эхо в пустом зале — подтверждают универсальность флуктуаций параметра порядка вблизи перехода БКТ. Однако, универсальность — лишь удобная иллюзия, позволяющая ненадолго упорядочить хаос. Истинная красота кроется в отклонениях, в тех шепотах аномалий, которые ускользают от внимания агрегатов усреднения. Следующим шагом представляется не углубление в математическую точность ренормгруппы, а поиск тех самых «неудобных» систем, где эта универсальность даёт сбой.

В особенности, стоит обратить внимание на динамику, далекую от равновесия. Резкое изменение параметров системы — не просто тест для модели, а возможность увидеть, как порядок рождается из хаоса, как флуктуации, освобожденные от оков равновесия, формируют новые, неожиданные структуры. Измерение полной функции распределения в этих условиях — задача нетривиальная, но именно там, в этой борьбе с шумом и неопределенностью, и кроется истинный прогресс.

Ведь любое приближение — это лишь заклинание, работающее до первого столкновения с реальностью. И, возможно, следующая «волшебная формула» потребует не более точного описания бозонного газа, а совершенно иного взгляда на природу порядка и хаоса.

Оригинал статьи: https://arxiv.org/pdf/2601.16204.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-23 15:51