Автор: Денис Аветисян
Исследователи разработали инновационный метод реконструкции наноразмерных магнитных структур по данным NV-магнитометрии, объединяющий дифференцируемое прямое моделирование с физически обоснованными ограничениями.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал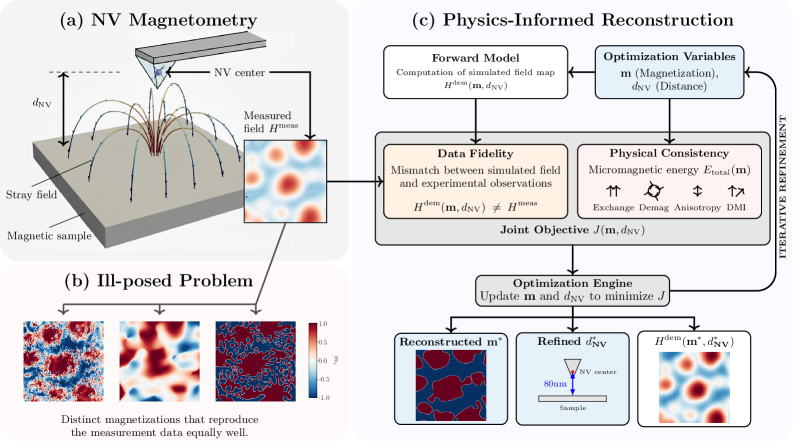
Представлен физически обоснованный фреймворк реконструкции, использующий преобразование Фурье для восстановления намагниченности и расстояния до сенсора на основе данных NV-центров.
Восстановление сложных магнитных текстур из измерений поля рассеяния, полученных с помощью азотных вакансий (NV-центров), представляет собой сложную обратную задачу. В данной работе, озаглавленной ‘A Fourier-Space Approach to Physics-Informed Magnetization Reconstruction from Nitrogen-Vacancy Measurements’, предложен физически обоснованный метод, включающий в вариационную формулировку полную микромагнитную энергию. Разработанная на базе PyTorch модель сочетает в себе дифференцируемый микромагнитный фреймворк, основанный на конечно-разностных схемах, с расчетом поля рассеяния в частотной области и продолжением вверх в пространстве Фурье, что позволяет одновременно реконструировать как намагниченность, так и расстояние до сенсора. Сможет ли данный подход открыть новые возможности для высокоточного анализа наноразмерных магнитных структур и расширить применение NV-магнитометрии?
Математическая Элегантность Обратной Задачи в Магнетизме
Восстановление конфигурации намагниченности по измеренным магнитным полям представляет собой основополагающую, но сложную обратную задачу в магнетизме. Эта задача, встречающаяся в различных областях, от анализа магнитных носителей информации до неразрушающего контроля материалов, требует определения распределения магнитных моментов внутри образца на основе данных, полученных внешними датчиками. Сложность возникает из-за того, что магнитное поле, измеренное вне образца, является интегральным результатом вклада от всех магнитных моментов внутри него, что затрудняет однозначное определение исходной конфигурации намагниченности. Точное решение этой задачи имеет решающее значение для понимания магнитных свойств материалов и разработки новых магнитных технологий, однако требует применения сложных математических методов и алгоритмов для преодоления присущих ей неопределенностей.
Проблема восстановления намагниченности из измеренных магнитных полей по своей природе является некорректно поставленной задачей. Это означает, что существует бесконечное количество различных распределений намагниченности, которые могут породить одно и то же наблюдаемое магнитное поле. Иными словами, однозначно определить исходное состояние намагниченности, опираясь исключительно на внешние измерения, невозможно. Для получения физически правдоподобного решения требуется применение методов регуляризации — специальных процедур, вводящих дополнительные ограничения или априорные знания о системе. Эти ограничения позволяют выбрать одно из множества возможных решений, наиболее соответствующее реальной физической ситуации и минимизирующее неопределенность, связанную с некорректностью задачи.
Первые методы реконструкции магнитной картины, такие как количественная магнитографическая микроскопия, представляли собой важный первоначальный шаг, однако столкнулись с существенными ограничениями при работе со сложными трехмерными структурами. Точность определения намагниченности оказывалась недостаточной из-за сложностей в моделировании взаимодействия магнитного поля с неоднородными образцами. Проблемой являлось не только разрешение приборов, но и трудности в корректном учете влияния геометрии образца на измеряемое поле, что приводило к артефактам и искажениям в реконструируемой магнитной конфигурации. В результате, получение достоверной картины намагниченности в сложных 3D-геометриях требовало разработки более совершенных алгоритмов и методов измерений.
Физически Обоснованный Подход к Реконструкции
Для решения проблемы неоднозначности в задачах реконструкции намагниченности, нами разработан фреймворк реконструкции, основанный на физических принципах. Данный подход предполагает непосредственное включение уравнений и концепций микромагнетизма в процесс оптимизации. Вместо поиска любого решения, удовлетворяющего данным полям, оптимизация проводится с учетом физических ограничений, что позволяет получать более стабильные и достоверные результаты, соответствующие реальным физическим свойствам магнитных материалов. Фреймворк позволяет встраивать в процесс оптимизации как уравнения, описывающие поведение намагниченности, так и энергетические функционалы, характеризующие стабильность магнитных состояний.
В рамках предлагаемой схемы восстановления используется концепция полной магнитной энергии E_{total} в качестве регуляризующего члена. Эта энергия складывается из нескольких компонент, описывающих различные физические взаимодействия в материале. В частности, энергия обмена E_{exchange} отражает взаимодействие между соседними магнитными моментами, энергия размагничивания E_{demagnetization} учитывает влияние формы образца и намагниченности, энергия одноосной анизотропии E_{uniaxial} определяет предпочтительное направление намагниченности, а энергия Дзялошинского-Мория E_{DMI} способствует формированию магнитных текстур, таких как доменные стенки и вихри. Минимизация полной магнитной энергии в процессе оптимизации обеспечивает получение физически правдоподобных состояний намагниченности, ограничивая пространство решений и повышая устойчивость реконструкции.
Минимизация как невязки поля, так и полной магнитной энергии ( E_{total} ) является ключевым элементом обеспечения физически правдоподобных состояний намагниченности. Невязка поля определяет, насколько хорошо реконструированная намагниченность соответствует измеренным данным поля. В то же время, минимизация полной магнитной энергии, включающей энергию обмена, размагничивания, одноосной анизотропии и взаимодействие Дзялошинского-Мория, ограничивает пространство решений, отбрасывая нефизические конфигурации. Этот подход эффективно сочетает соответствие данным с физическими ограничениями, позволяя получить стабильные и реалистичные результаты реконструкции намагниченности.
Для обеспечения физически корректного и непротиворечивого решения в процессе реконструкции магнитной структуры используется уравнение Лапласа, моделирующее скалярный магнитный потенциал \nabla^2 \phi = 0. Данное уравнение описывает поведение магнитного поля в отсутствие источников, что соответствует физической реальности большинства магнитных материалов. Использование уравнения Лапласа позволяет связать магнитное поле с магнитной индукцией и гарантирует, что решение будет удовлетворять дивергенции, равной нулю \nabla \cdot \mathbf{B} = 0, что является фундаментальным требованием для магнитных полей. Применение данного подхода обеспечивает согласованность между данными измерений и реконструируемой магнитной структурой, предотвращая появление нефизичных решений.
Строгий Алгоритмический Подход к Валидации
В рамках нашей системы используется риманова оптимизация для обеспечения нормализации намагниченности, что гарантирует физически реалистичные решения на единичной сфере. Данный метод позволяет эффективно решать задачу оптимизации, наложенную ограничением, что вектор намагниченности должен лежать на единичной сфере S^2. В отличие от стандартных алгоритмов оптимизации, риманова оптимизация учитывает геометрию сферы, что предотвращает отклонения от физически допустимых состояний и обеспечивает стабильность процесса реконструкции. Ограничение на единичную сферу реализуется через проекцию градиента на касательное пространство сферы, что позволяет избежать нарушения условия нормализации в процессе итераций.
Метод сопряжённых градиентов, в сочетании с регуляризацией Тихонова, позволяет эффективно проводить градиентную оптимизацию для трёхмерной реконструкции намагниченности. Метод сопряжённых градиентов значительно снижает вычислительную сложность по сравнению с прямым вычислением градиента, что критически важно для задач с большим объёмом данных. Регуляризация Тихонова, добавляющая к целевой функции член \lambda ||x||^2 , где λ — параметр регуляризации, а x — решение, стабилизирует процесс оптимизации и предотвращает переобучение, особенно в условиях неполноты или зашумлённости данных. Комбинация этих методов обеспечивает быструю сходимость и получение стабильных, физически правдоподобных решений при реконструкции трёхмерных распределений намагниченности.
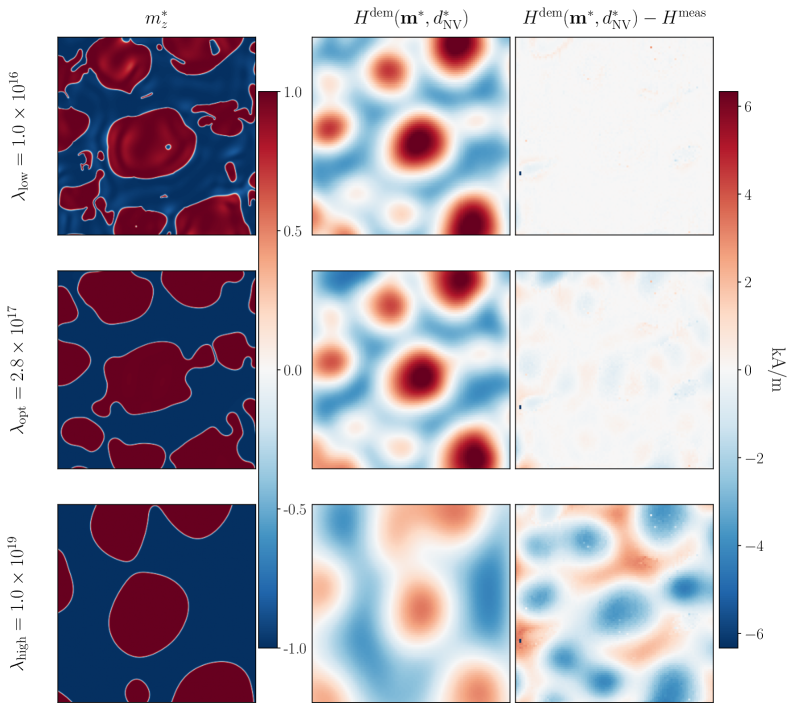
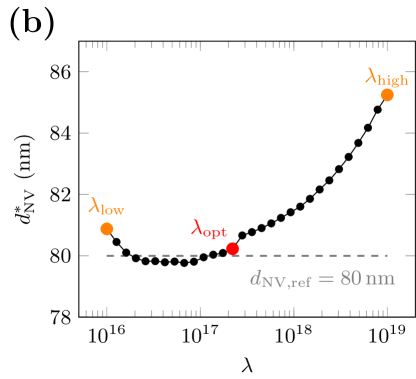
Для определения оптимального параметра регуляризации при реконструкции намагниченности использовался метод L-кривой. Данный метод позволяет достичь баланса между точностью соответствия реконструированного решения экспериментальным данным и гладкостью полученного решения. В результате применения метода L-кривой были получены следующие оптимальные значения параметра регуляризации: 2.2 \times 10^{17} для синтетических данных и 2.8 \times 10^{17} для экспериментальных данных. Выбор данных значений обеспечивает стабильность и достоверность результатов реконструкции, минимизируя влияние шумов и артефактов.
Средняя абсолютная ошибка (Mean Absolute Error, MAE) используется в качестве надежной метрики для оценки точности реконструкции магнитных полей. Данный показатель количественно определяет разницу между реконструированным и измеренным полями, вычисляясь как среднее значение абсолютных разностей между соответствующими точками данных. Использование MAE позволяет оценить величину систематических и случайных ошибок реконструкции, предоставляя объективную оценку качества полученного решения и его соответствия экспериментальным данным. Низкое значение MAE свидетельствует о высокой точности реконструкции и хорошем согласии между моделью и реальностью.
Влияние и Перспективы Развития Метода
Разработанный метод реконструкции магнитного поля обладает значительным потенциалом для решения обратной задачи в более широком спектре сценариев, включая те, которые характеризуются топологическими ограничениями. Это означает, что алгоритм способен не только восстановить пространственное распределение магнитного поля по данным измерений, но и учитывать сложные магнитные структуры, такие как домены и вихри, определяемые специфическими топологическими свойствами материала. Возможность работы с топологическими ограничениями открывает перспективы для изучения и моделирования сложных магнитных текстур в материалах с нетривиальной топологией, что особенно важно для развития новых магнитных устройств и сенсоров. Перспективы включают в себя моделирование магнитных монополей и спинтронных устройств с улучшенными характеристиками, расширяя границы применимости метода за пределы традиционных задач магнитной микроскопии.
Для значительного ускорения процесса реконструкции магнитных текстур активно применяются методы, основанные на преобразовании Фурье. Переход в частотную область позволяет эффективно анализировать и обрабатывать данные, поскольку многие операции, сложные в пространственной области, упрощаются и становятся вычислительно менее затратными в частотной. Этот подход особенно полезен при работе с большими объемами данных, характерными для современных магнитометрических исследований. Преобразование Фурье позволяет выделить ключевые частотные компоненты, отвечающие за структуру магнитных текстур, и быстро восстановить пространственное распределение магнитных полей, что существенно сокращает время вычислений и повышает эффективность алгоритмов реконструкции.
Для эффективной генерации начальных приближений при решении обратной задачи магнетизма используются физически обоснованные нейронные сети, объединяющие архитектуру U-Net и метод микромагнитной релаксации. Такой подход позволяет учитывать физические ограничения и особенности исследуемых магнитных структур, значительно ускоряя и повышая точность реконструкции. Архитектура U-Net, благодаря своей способности захватывать как локальные, так и глобальные особенности данных, в сочетании с микромагнитной релаксацией, моделирующей поведение магнитных доменов, создает реалистичные и физически правдоподобные начальные условия для последующей оптимизации. В результате, данный метод демонстрирует превосходство над традиционными подходами, требующими ручного задания начальных параметров или использования менее точных моделей.
Магнитометрия с использованием азотных вакансий (NV-центров) предоставила измерения с высоким разрешением, необходимые для проверки и уточнения предсказаний разработанной схемы реконструкции. Этот метод, основанный на чувствительности NV-центров к магнитным полям, позволил добиться сходимости к точно реконструированной высоте сенсора, составляющей приблизительно 75-80 нанометров. Такая точность является критически важной для дальнейшего развития наносенсоров и магнитных систем, открывая возможности для детального изучения магнитных текстур и топологических особенностей на наноуровне. Полученные результаты демонстрируют перспективность использования NV-магнитометрии в качестве ключевого инструмента для валидации и оптимизации алгоритмов реконструкции, обеспечивая основу для создания более точных и надежных магнитных изображений.

Представленное исследование демонстрирует стремление к математической чистоте в решении сложной задачи реконструкции намагниченности. Подход, сочетающий дифференцируемую прямую модель с микромагнитными энергетическими членами, представляет собой элегантный способ одновременной реконструкции намагниченности и расстояния до сенсора. Это не просто стремление к практическому результату, но и к созданию алгоритма, который можно доказать, а не просто проверить на тестовых данных. Как однажды заметила Симона де Бовуар: «Старость — это не столько физическое состояние, сколько вопрос восприятия». В данном контексте, «старость» можно метафорически применить к алгоритмам — лишь тщательно выстроенный, математически обоснованный подход остаётся актуальным и масштабируемым, в отличие от эмпирических решений, которые со временем теряют свою ценность.
Что дальше?
Представленный подход, хотя и демонстрирует потенциал в реконструкции намагниченности на основе данных NV-магнитометрии, не является панацеей. Очевидным ограничением остаётся вычислительная сложность, особенно при увеличении разрешения реконструируемой области. Простое увеличение количества итераций градиентной оптимизации не решит проблему — необходимы принципиально новые алгоритмические решения, возможно, основанные на спектральных методах или разреженных представлениях. Иначе, в погоне за деталями, рискуем утонуть в вычислительном шуме.
Более того, следует признать, что точная физическая модель демагнетизирующего поля, используемая в работе, является упрощением. Реальные микромагнитные структуры, особенно в неоднородных материалах, могут демонстрировать гораздо более сложные взаимодействия. Вместо слепого добавления все новых и новых параметров в модель, представляется более перспективным путь поиска инвариантных характеристик, нечувствительных к мелким деталям структуры. Истинная элегантность алгоритма проявляется не в способности “подгоняться” под любые данные, а в способности выявлять фундаментальные закономерности.
В конечном счёте, успех данного направления исследований будет определяться не столько совершенством численных методов, сколько способностью к строгому математическому обоснованию полученных результатов. В хаосе данных спасает только математическая дисциплина. Построение алгоритма, чья сходимость и устойчивость могут быть доказаны, — вот та задача, которая действительно достойна внимания.
Оригинал статьи: https://arxiv.org/pdf/2602.17180.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Решение головоломки с паролем Absolum в Yeldrim.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Все коды в Poppy Playtime Глава 4
- YAPYAP Список заклинаний
- Акции VTBR. Банк ВТБ: прогноз акций.
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Прогнозы криптовалюты MYX: информация о ценах на MYX
- Доллар обгонит вьетнамский донг? Эксперты раскрыли неожиданный сценарий
- Объяснение каждого Таргариена в «Рыцаре семи королевств»
- Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?
2026-02-22 16:19