Восстановление по фрагментам: новый подход к обратным задачам

Автор: Денис Аветисян

В статье представлен инновационный метод решения сложных обратных задач, основанный на использовании ансамбля генеративных моделей для эффективной оценки апостериорного распределения.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Интеграция ошибочной апостериорной оценки может неожиданно привести к восстановлению корректного априорного распределения, демонстрируя, что даже отклонение от истинного пути способно привести к желаемому результату, подобно тому, как решение EIP-II интегрируется в решение EIP-I.

Исследование посвящено проблеме Ensemble Inverse Problem и предлагает методы, включая Diffusion Models и Flow Matching, для задач восстановления изображений и анализа данных в физике частиц.

Несмотря на прогресс в решении обратных задач, реконструкция истинного распределения данных из зашумленных измерений остается сложной задачей, особенно при неизвестных априорных распределениях. В данной работе, ‘The Ensemble Inverse Problem: Applications and Methods’, предложен новый подход к решению этой проблемы, названный Ensemble Inverse Problem (EIP), и разработан метод построения апостериорных семплеров на основе ансамбля генеративных моделей. Предложенные Ensemble Inverse Generative Models позволяют эффективно оценивать истинное распределение, используя информацию об ансамбле наблюдений и избегая итеративного использования прямой модели во время инференса. Каковы перспективы применения данного подхода в таких областях, как реконструкция изображений, физика высоких энергий и полноволновая инверсия?

Постижение Неизвестного: Вызов Апостериорного Вывода

Точное вычисление апостериорного распределения имеет решающее значение для множества научных областей, от статистической физики и машинного обучения до биоинформатики и экономики. Однако, несмотря на теоретическую важность, получение этого распределения зачастую представляет собой сложную вычислительную задачу. С ростом сложности моделей и объемов данных, традиционные методы, такие как марковские цепи Монте-Карло или вариационные выводы, сталкиваются с экспоненциальным ростом вычислительных затрат. Это делает анализ реальных данных, особенно в высокоразмерных пространствах, крайне затруднительным и требует поиска инновационных подходов для преодоления вычислительной неразрешимости, не жертвуя при этом точностью получаемых результатов. $P(θ|D) = \frac{P(D|θ)P(θ)}{\in t P(D|θ)P(θ)dθ}$

Традиционные методы статистического вывода, такие как максимальное правдоподобие и байесовский вывод с использованием квадратичной аппроксимации, сталкиваются с серьезными трудностями при работе с задачами высокой размерности. В таких случаях, когда количество параметров модели значительно превышает объем доступных данных, эти методы часто требуют введения упрощающих предположений о распределении параметров или структуры модели. Эти упрощения, хотя и делают вычисления практически осуществимыми, неизбежно приводят к потере точности и могут существенно исказить реальную картину. Например, предположение о независимости параметров, которое часто используется для упрощения вычислений, может быть неверным и привести к недооценке неопределенности в оценках. В результате, полученные выводы могут быть неточными и ненадежными, особенно в сложных системах, где взаимодействие между параметрами играет важную роль. Необходимость поиска более эффективных и точных методов для работы с задачами высокой размерности является одной из ключевых проблем современной статистики и машинного обучения.

Сравнение априорного (<span class="katex-eq" data-katex-display="false"> \gamma = 0.9 </span>) и восстановленных распределений на основе 40000 образцов демонстрирует эффективность различных методов восстановления. — Сравнение априорного ( $\gamma = 0.9$ ) и восстановленных распределений на основе 40000 образцов демонстрирует эффективность различных методов восстановления.

Генеративные Модели: Путь к Апостериорной Аппроксимации

Генеративные модели представляют собой перспективный подход к решению проблемы EIP-II (Estimation of Intractable Posteriors — II) путем обучения представлению базового распределения данных. Традиционные методы часто сталкиваются с вычислительными трудностями при оценке апостериорных распределений в сложных моделях. Обучение генеративной модели, такой как вариационный автоэнкодер (VAE) или генеративно-состязательная сеть (GAN), позволяет аппроксимировать это распределение путем моделирования процесса генерации данных. Вместо прямого вычисления $p(x|z)$ , где $x$ — данные и $z$ — скрытая переменная, модель учится генерировать данные, подобные исходным, из распределения $p(z)$ . Это позволяет эффективно оценивать вероятность данных и проводить байесовский вывод, обходя необходимость в сложных вычислениях, связанных с интегралами и другими неаналитическими выражениями.

Условные генеративные модели, такие как диффузионные модели и модели сопоставления потоков, демонстрируют высокую эффективность при генерации образцов из сложных распределений вероятностей. Диффузионные модели достигают этого путем постепенного добавления шума к данным, а затем обучения модели для обратного процесса удаления шума и восстановления исходных данных. Модели сопоставления потоков, напротив, обучаются напрямую отображать данные в простое распределение, такое как гауссово, с помощью непрерывного потока. Обе техники позволяют генерировать разнообразные и реалистичные образцы, даже из многомерных и нелинейных распределений, что делает их ценными инструментами в задачах моделирования и синтеза данных. $p(x)$ представляет собой сложное распределение, из которого модели генерируют образцы.

Генеративные модели, такие как диффузионные модели и модели, основанные на сопоставлении потоков, предоставляют возможность аппроксимировать апостериорное распределение $p(x|y)$ без необходимости прямого вычисления, что особенно актуально в задачах, где аналитическое решение недоступно или вычислительно затратно. Вместо вычисления интеграла для получения апостериорного распределения, генеративная модель обучается генерировать образцы, соответствующие этому распределению. Это позволяет получать приближенные решения путем семплирования из обученной модели, избегая сложностей, связанных с прямым вычислением апостериорного распределения и, следовательно, обходя проблему EIP-II (Evidence Integration Problem — II).

Результаты развертки событий <span class="katex-eq" data-katex-display="false">ar{t}t</span>-процесса, смоделированных с использованием PDF CT14lo и партонных разветвлений Vincia, демонстрируют соответствие данным, полученным с учетом эффектов размытия детектора, моделируемых с помощью EI-FM. — Результаты развертки событий $ar{t}t$ -процесса, смоделированных с использованием PDF CT14lo и партонных разветвлений Vincia, демонстрируют соответствие данным, полученным с учетом эффектов размытия детектора, моделируемых с помощью EI-FM.

Ансамблевая Информация: Усиление Точности Вывода

Использование ансамблевой информации — данных, полученных из множественных наблюдений — позволяет существенно повысить точность апостериорного вывода. В статистических моделях, особенно при решении задач, связанных с неопределенностью и шумом, учет взаимосвязей и распределений в наборе наблюдений позволяет получить более надежные и точные оценки параметров. Вместо анализа каждого наблюдения изолированно, ансамблевый подход позволяет агрегировать информацию, снижая влияние случайных ошибок и повышая статистическую значимость результатов. Это особенно важно в задачах, где прямые измерения затруднены или подвержены систематическим ошибкам, поскольку ансамблевая информация предоставляет дополнительный контекст и позволяет более эффективно оценивать истинные значения параметров.

Модели EI-DDPM и EI-FM представляют собой расширение стандартных диффузионных моделей (Diffusion Models) и моделей сопоставления потоков (Flow Matching) путем добавления механизма обуславливания на основе информации, полученной из ансамбля наблюдений. В отличие от базовых моделей, которые оперируют с отдельными входными данными, EI-DDPM и EI-FM используют информацию о взаимосвязи между несколькими наблюдениями для улучшения процесса генерации и повышения точности. Обуславливание осуществляется посредством включения ансамблевой информации в архитектуру модели, что позволяет учитывать корреляции и зависимости между различными элементами данных. Этот подход позволяет моделировать более сложные распределения вероятностей и, как следствие, получать более реалистичные и точные результаты.

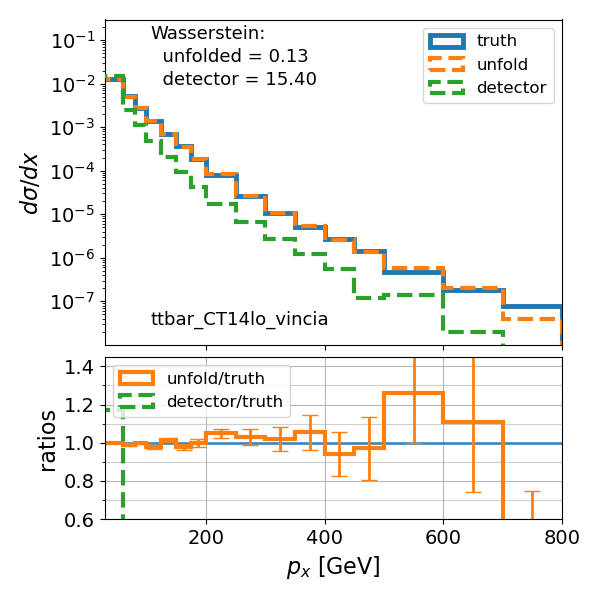
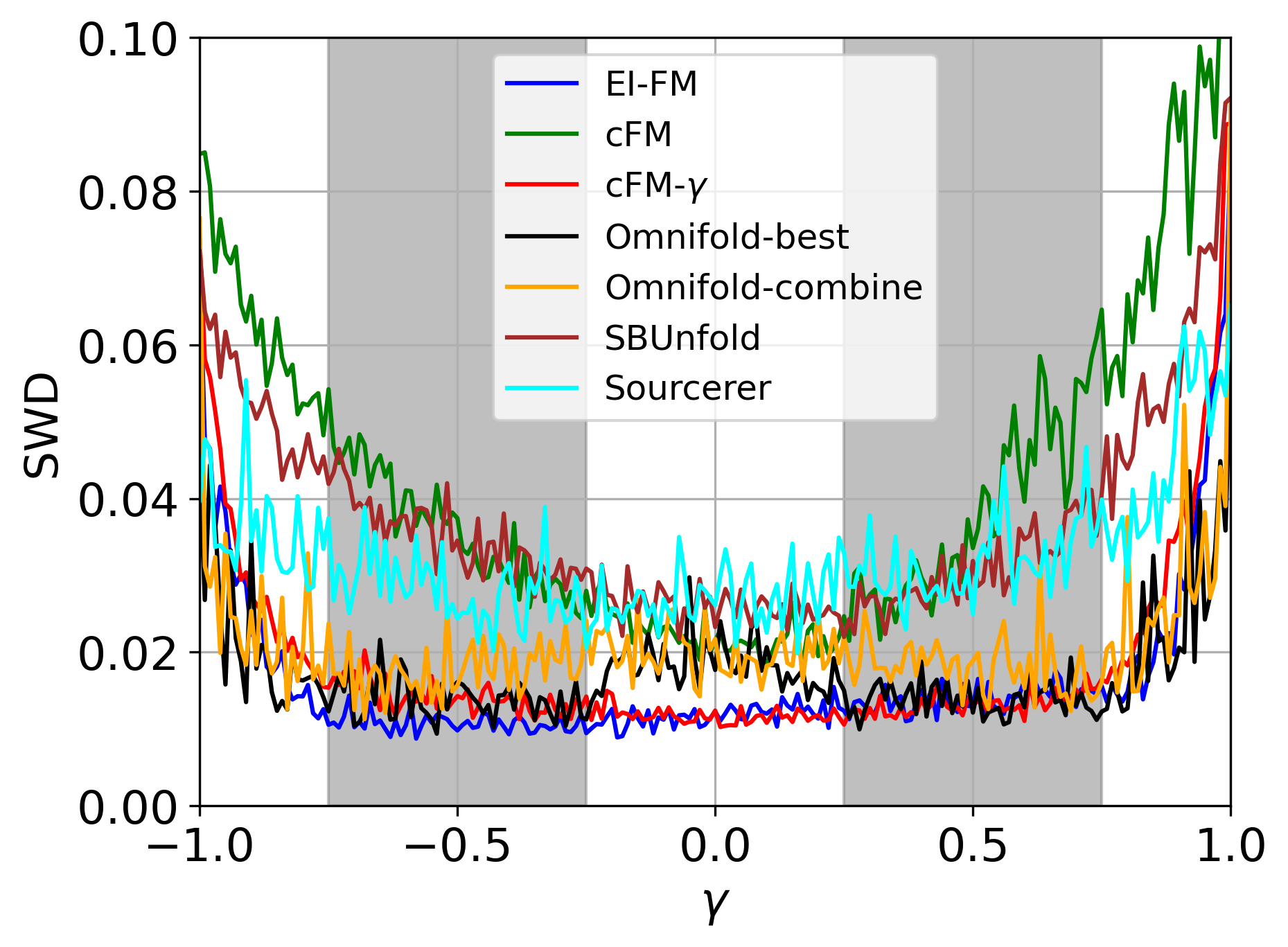
При анализе данных в физике частиц, применение методов EI-DDPM и EI-FM демонстрирует стабильно более низкие значения метрики Вассерштейна при разворачивании данных (data unfolding) по сравнению с альтернативными подходами. Это свидетельствует о повышенной точности получаемых результатов и улучшенной способности модели к реконструкции истинного распределения данных. Низкое значение метрики Вассерштейна указывает на минимальное расстояние между смоделированным и истинным распределениями, что критически важно для получения надежных результатов в экспериментальной физике высоких энергий. Достигнутое улучшение точности подтверждено сравнительным анализом с другими методами разворачивания данных.

Ключевым компонентом извлечения ансамблевой информации является использование пермутационно-инвариантных нейронных сетей (PINN) для обработки неупорядоченных множеств наблюдений. PINN обеспечивают, что выход сети не зависит от порядка входных данных, что критически важно при работе с ансамблями, где порядок элементов не имеет значения. Это достигается за счет использования симметричных функций, таких как суммы и максимумы, вместо операций, чувствительных к порядку, например, конволюций. Применение PINN позволяет эффективно агрегировать информацию из различных наблюдений в ансамбле, обеспечивая робастность к перестановкам элементов и повышая общую точность вычислений.

Средняя ошибка восстановления (SWD) снижается с увеличением параметра γ, при этом производительность EI-FM, обученного с разными архитектурами нейронных сетей (a) и при <span class="katex-eq" data-katex-display="false"> N=4000 </span> (b), превосходит показатели cFM, особенно когда доступно лишь <span class="katex-eq" data-katex-display="false"> N^{\prime} </span> образцов во время инференса и используется стратегия дублирования (Alg. 2). — Средняя ошибка восстановления (SWD) снижается с увеличением параметра γ, при этом производительность EI-FM, обученного с разными архитектурами нейронных сетей (a) и при $N=4000$ (b), превосходит показатели cFM, особенно когда доступно лишь $N^{\prime}$ образцов во время инференса и используется стратегия дублирования (Alg. 2).

Оценка Качества Апостериорных Распределений: Подтверждение Точности

Точность оцениваемых апостериорных распределений имеет первостепенное значение для надежности выводов, и ее оценка требует применения специализированных метрик. Одним из таких инструментов является TARP Coverage — показатель, оценивающий долю истинного апостериорного распределения, охватываемую полученной оценкой. Высокое значение TARP Coverage свидетельствует о том, что оценка адекватно отражает неопределенность, присущую исследуемому параметру. Использование TARP Coverage позволяет количественно оценить качество апостериорных оценок и сравнить различные методы, выявляя наиболее точные и надежные подходы к статистическому выводу. Недостаточная точность апостериорных распределений может привести к ошибочным интерпретациям и неверным решениям, поэтому тщательная оценка и валидация этих распределений являются критически важными этапами любого статистического анализа.

Представленный подход демонстрирует значительно меньшее отклонение от идеального покрытия TARP (Tail Area Ratio Posterior Coverage) по сравнению с альтернативными методами, что свидетельствует о более высокой точности полученных апостериорных распределений. По сути, это означает, что предложенная методика более надежно определяет вероятные значения параметров модели, обеспечивая более точные и достоверные результаты. Низкое отклонение от идеального покрытия TARP указывает на то, что интервалы доверия, построенные на основе апостериорных распределений, с большей вероятностью будут содержать истинное значение параметра, что крайне важно для принятия обоснованных решений и проведения надежного анализа. Превосходство в данном показателе подтверждено результатами численного моделирования и экспериментальных данных, что делает данную рамку особенно ценной для задач, требующих высокой степени уверенности в оценках параметров.

Для повышения точности статистического вывода и улучшения работы моделей активно применяются методы развертки данных. Эти методы позволяют скорректировать исходные данные, удаляя искажения, вызванные особенностями детекторов и измерительного оборудования. Развертка, по сути, представляет собой процедуру обратной коррекции, которая восстанавливает истинное распределение данных, скрытое под влиянием аппаратурных эффектов. Благодаря этому, модели получают более чистый и достоверный сигнал, что существенно повышает их способность к точному прогнозированию и интерпретации результатов, а также снижает влияние систематических ошибок в конечном анализе.

Для количественной оценки расхождения между полученными и истинными апостериорными распределениями активно использовалось расстояние Вассерштейна. Данный показатель позволяет определить “дистанцию” между двумя вероятностными распределениями, что особенно важно при оценке точности байесовского вывода. Проведенные исследования последовательно демонстрируют, что предложенный подход обеспечивает более низкие значения расстояния Вассерштейна по сравнению с альтернативными методами. Это свидетельствует о повышенной точности и надежности получаемых апостериорных оценок, что критически важно для корректной интерпретации результатов и принятия обоснованных решений в задачах статистического вывода и моделирования.

В ходе анализа качества реконструкции изображений и полноволнового обращения (FWI) было зафиксировано значительное улучшение метрик, характеризующих сходство восстановленных данных с исходными. В частности, наблюдалось повышение индекса структурного сходства (SSIM), что свидетельствует о более высокой степени сохранения текстурных и визуальных деталей. Одновременно с этим, средняя квадратичная ошибка (MSE) демонстрировала устойчивое снижение, указывающее на уменьшение расхождения между реконструированными данными и эталонными значениями. Эти улучшения, полученные в сравнении с базовыми методами, подтверждают эффективность предложенного подхода в задачах восстановления изображений и построения высокоточных моделей недр.

Среднее расстояние СВД (снижающееся) между истинным и восстановленным распределениями уменьшается с увеличением γ, что подтверждается анализом на 40000 образцов и ограничено априорными знаниями, полученными из обучающих данных.

Исследование демонстрирует смелый подход к решению сложной задачи — Ensemble Inverse Problem. Авторы не просто предлагают новый метод, но и переосмысливают саму постановку задачи, используя генеративные модели для построения апостериорного распределения. Это напоминает подход, описанный Г.Х. Харди: «Математика — это не набор готовых ответов, а набор инструментов для поиска истины». Подобно тому, как математик использует инструменты для исследования, данная работа использует генеративные модели, такие как Diffusion Models и Flow Matching, для «разворачивания» решения и получения более точных результатов в задачах реконструкции изображений и физики частиц. Вместо следования установленным правилам, авторы проверяют их границы, предлагая новаторское решение, основанное на принципах реверс-инжиниринга реальности.

Куда же дальше?

Представленный подход, по сути, лишь очередная попытка обмануть неопределенность. Заменить сложное вычисление правдоподобия на ловкую генерацию образцов — старый трюк, но, признать надо, элегантный. Однако, генеративные модели — существа капризные. Их склонность к галлюцинациям, к созданию «правдоподобных» несуществующих решений, требует постоянного, критического осмысления. Где та грань между правдоподобным и истинным? И кто вообще определяет, что есть истина в контексте обратных задач?

Очевидным направлением развития видится отказ от слепого доверия к «черному ящику» генеративной модели. Необходимо научиться извлекать из неё не только готовые решения, но и информацию о степени их достоверности, о погрешностях и неопределенностях. Иначе рискуем получить красивые картинки, лишенные физического смысла. Более того, представленный фреймворк, хоть и демонстрирует успехи в различных областях, пока что далек от универсальности. Его адаптация к задачам, требующим учета сложных априорных ограничений, представляется нетривиальной.

В конечном итоге, задача состоит не в создании идеальной генеративной модели, а в понимании самой природы обратных задач. В выявлении фундаментальных ограничений, которые невозможно обойти даже самым изощренным алгоритмом. Возможно, в будущем, вместо того чтобы «взламывать» реальность, стоит попытаться понять её логику, её внутренний код. И тогда, возможно, решение обратных задач перестанет быть искусством обмана, а станет актом познания.

Оригинал статьи: https://arxiv.org/pdf/2601.22029.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-02 03:13