Ядро в фокусе: Новый метод для изучения неустойчивых состояний

Автор: Денис Аветисян

Исследователи разработали усовершенствованный алгоритм для точного расчета широких многочастичных резонансов в легких ядрах, открывая новые возможности для понимания структуры атомных ядер.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Мнимые части собственных значений матрицы плотности для основного состояния гелия-5 демонстрируют зависимость от добавляемой орбитали, полученную в рамках G-DMRG расчётов, что позволяет исследовать структуру и свойства этого экзотического атома.

Работа посвящена развитию метода Гамова ренормированной матрицы плотности (G-DMRG) для моделирования неустойчивых состояний в ядерной физике.

Несмотря на значительный прогресс в $\textit{ab initio}$ ядерной теории, предсказание границ стабильности ядер остается сложной задачей из-за неопределенностей в ядерных силах и трудностей в описании открытых квантовых систем. В настоящей работе, посвященной исследованию ‘Ab initio Gamow density matrix renormalization group for broad nuclear many-body resonances’, предложены усовершенствования в методе Гамова ренормгруппы матрицы плотности (G-DMRG), позволяющие эффективно рассчитывать широкие многочастичные резонансы в легких ядрах. Ключевым достижением является разработка новых схем усечения базиса и упорядочивания орбит, основанных на анализе запутанности, что обеспечивает сходимость расчетов и позволяет провести первое $\textit{ab initio}$ вычисление основного состояния $^{1/2^+}$ ядра $^5\text{H}$ . Какие еще возможности открываются для применения усовершенствованного G-DMRG метода в исследовании экзотических ядер и ядерных реакций?

Широкие Резонансы: Вызов Современной Ядерной Физики

Традиционные методы квантовой механики испытывают значительные трудности при описании резонансных состояний, особенно тех, которые характеризуются большой шириной распада — так называемые $BroadManyBodyResonances$ . Эти состояния, возникающие в сложных системах, таких как атомные ядра, представляют собой кратковременные возбуждения, быстро распадающиеся на другие частицы. Проблема заключается в том, что стандартные подходы, основанные на понятии собственных состояний с определенной энергией, не позволяют адекватно учесть быстрый процесс распада и широкую энергетическую неопределенность. Это препятствует точному моделированию ядерных реакций, процессов рассеяния и, в конечном итоге, пониманию структуры и свойств атомных ядер. Точное описание $BroadManyBodyResonances$ требует разработки новых теоретических инструментов, способных учитывать негерметичность квантовых систем и динамику распада, что является ключевой задачей современной ядерной физики.

Резонансные состояния играют фундаментальную роль в понимании процессов рассеяния и передачи энергии в сложных системах, однако их природа, характеризующаяся широкими ширинами затухания и сложной внутренней структурой, требует принципиально нового теоретического подхода. Традиционные методы квантовой механики, основанные на эрмитовности операторов, оказываются недостаточными для адекватного описания этих состояний, поскольку не позволяют напрямую учитывать динамику затухания и смешивания различных конфигураций. Для точного моделирования резонансов необходимо разрабатывать теории, выходящие за рамки стандартного формализма, и учитывать неэрмитовы эффекты, что открывает новые перспективы в исследовании ядерной структуры и реакций, а также в других областях физики, где процессы рассеяния и передачи энергии имеют ключевое значение. Разработка адекватной теоретической базы позволит не только предсказывать свойства резонансов, но и управлять ими, что может привести к созданию новых технологий и материалов.

Для адекватного описания динамики распада резонансных состояний в сложных системах требуется отход от традиционных принципов эрмитовой квантовой механики. В то время как эрмитова квантовая механика прекрасно описывает стабильные состояния, она сталкивается с трудностями при моделировании состояний с конечным временем жизни, поскольку не позволяет напрямую учитывать явное исчезновение состояния во времени. Для преодоления этих ограничений разрабатываются альтернативные подходы, включающие использование неэрмитовых операторов Гамильтона и комплексного масштабирования энергии. Эти методы позволяют описывать распад как естественную часть эволюции системы, вводя мнимую часть энергии, пропорциональную ширине распада Γ. Такой подход позволяет более точно моделировать процессы рассеяния и передачи энергии в ядерной физике и других областях, где резонансные состояния играют ключевую роль, открывая возможности для углубленного понимания структуры и реакционной способности сложных систем.

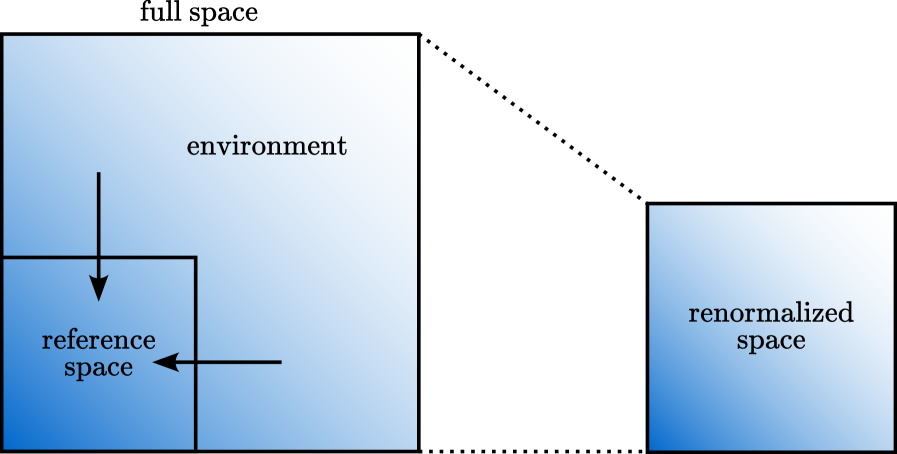
В оригинальной формулировке DMRG вильсоновская ренормализация Гамильтониана позволяет «включить» влияние окружающей среды, аппроксимируя исходный Гамильтониан в ренормализованном пространстве.

Gamow-DMRG: Комплексно-Энергетическое Решение

Группа Гамова-DMRG (G-DMRG) представляет собой расширение хорошо зарекомендовавшего себя метода DMRG для работы с комплексными энергиями. Это позволяет описывать резонансы как квазистационарные состояния, что принципиально отличает G-DMRG от стандартного DMRG, который оперирует с вещественными энергиями. Использование комплексных энергий позволяет корректно учитывать процессы распада резонансных состояний и получать информацию о ширине резонанса, что невозможно при анализе с использованием только вещественных энергий. В отличие от методов, которые аппроксимируют резонансы, G-DMRG позволяет численно решать уравнение Шрёдингера с комплексными энергиями, обеспечивая более точное и полное описание резонансных явлений в многочастичных системах.

Метод Gamow-DMRG обеспечивает точное описание динамики распада резонансных состояний благодаря использованию `ComplexEnergyGamowStates` и базиса Берггрена (`BerggrenBasis`). В отличие от традиционных методов, которые испытывают трудности с адекватным описанием распадающих состояний, G-DMRG позволяет напрямую рассчитывать комплексные энергии, соответствующие ширине распада резонанса. Базис Берггрена, представляющий собой набор дискретных состояний, связанных с непрерывным спектром, позволяет корректно учитывать влияние континуума на распад резонанса и обеспечивает численно стабильное решение уравнения Шрёдингера с комплексной энергией. Это позволяет точно определить время жизни резонанса и амплитуду его распада по различным каналам.

Метод Gamow-DMRG использует формализм квазистационарных состояний (QuasiStationaryFormalism) для упрощения многочастичной задачи. Этот подход позволяет эффективно вычислять резонансные состояния, рассматривая их как квазистационарные, а не строго стационарные решения уравнения Шрёдингера. В рамках этого формализма, волновая функция резонанса представляется как суперпозиция стационарных состояний с комплексными энергиями, что позволяет учесть процессы распада и ширину резонанса. В частности, это достигается путем решения обобщенного уравнения Гельмгольца с комплексным импульсом, что позволяет получить комплексные собственные значения энергии $E_n$ , где мнимая часть $Im(E_n)$ соответствует скорости распада состояния. Применение данного формализма значительно снижает вычислительные затраты при моделировании резонансов в сложных квантовых системах.

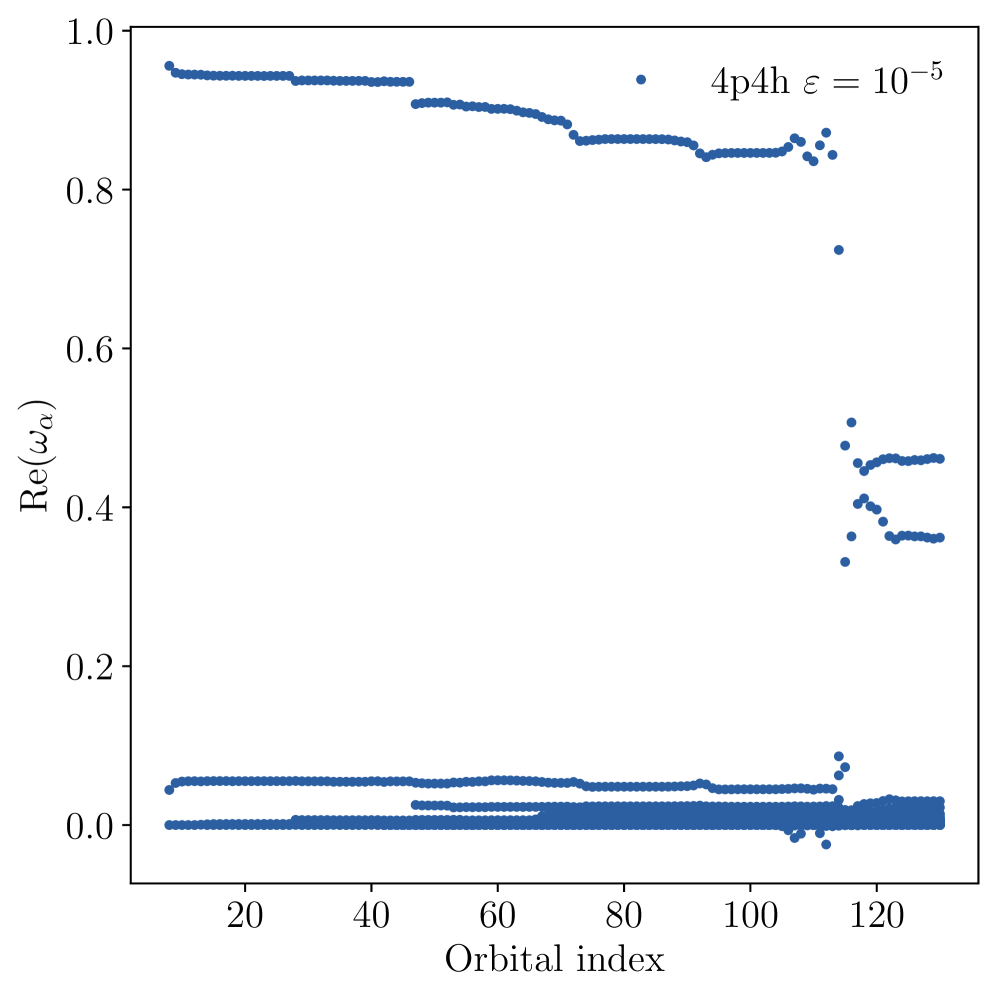
В расчетах G-DMRG реальная часть собственных значений матрицы плотности для основного состояния <span class="katex-eq" data-katex-display="false">H_4</span> зависит от добавленной орбитали. — В расчетах G-DMRG реальная часть собственных значений матрицы плотности для основного состояния $H_4$ зависит от добавленной орбитали.

Оптимизация G-DMRG для Точности и Эффективности

Эффективное решение многочастичной задачи в рамках G-DMRG требует стратегического построения `ReferenceSpace` (опорного пространства), направленного на фокусировку на наиболее релевантных степенях свободы. Выбор оптимального `ReferenceSpace` критически важен для снижения вычислительных затрат и обеспечения сходимости алгоритма. Необходимо выбирать базисные функции и конфигурации, которые в наибольшей степени влияют на энергетические уровни и свойства системы, отбрасывая несущественные детали. Это достигается путем анализа корреляционных эффектов и выбора конфигураций, описывающих основные типы возбуждений, а также использованием подходящих симметрий для уменьшения размерности пространства состояний. Некорректный выбор `ReferenceSpace` может привести к расходимости алгоритма или неточным результатам, требующим значительного увеличения вычислительных ресурсов.

Использование базиса естественных орбиталей (Natural Orbital Basis) значительно повышает скорость сходимости и снижает вычислительные затраты в G-DMRG. Вместо использования стандартного базиса, состоящего из одночастичных орбиталей, базис естественных орбиталей конструируется на основе собственных векторов матрицы плотности. Это позволяет эффективно отсекать наименее важные орбитали, концентрируя вычислительные ресурсы на наиболее значимых степенях свободы системы. Фактически, базис естественных орбиталей обеспечивает оптимальное представление волновой функции в заданном базисном пространстве, минимизируя ошибку усечения и ускоряя сходимость итерационных процедур. Эффективность подхода возрастает с увеличением размера системы и усложнением модели, делая его критически важным для расчетов в области ядерной физики и квантовой химии.

В основе DMRG и G-DMRG лежит процедура Вильсоновской ренормализации, которая систематически уменьшает вычислительную сложность многочастичной задачи. Этот метод заключается в последовательном исключении наименее значимых степеней свободы, позволяя эффективно описывать систему, фокусируясь на наиболее важных взаимодействиях. В результате, сложность решаемой задачи снижается экспоненциально с увеличением числа исключенных состояний, что позволяет проводить расчеты для систем большего размера, недоступных для традиционных методов, сохраняя при этом высокую точность результатов. Процесс ренормализации позволяет отобрать подпространство Хильберта, необходимое для адекватного описания физических свойств системы, и отбросить избыточные степени свободы, не оказывающие существенного влияния на результат.

В основе реализации G-DMRG лежит представление состояний с использованием $\mathbb{C}^{N \times N}$ комплексных симметричных матриц плотности, что необходимо для корректного описания энергетических уровней, включающих комплексные значения. Такой подход позволяет адекватно учитывать вклады различных конфигураций в волновой функции, даже если соответствующие энергии являются комплексными. Использование симметричных матриц плотности гарантирует эрмитовость гамильтониана и физическую корректность результатов. Эффективное хранение и манипулирование этими матрицами является ключевым фактором производительности алгоритма, особенно при работе с системами большого размера.

В данной работе впервые успешно применены ab initio вычисления в рамках G-DMRG для описания широких многочастичных резонансов в легких ядрах. Достигнута сходимость результатов для систем $He^4$ , $H^4$ и $H^5$ , что подтверждает применимость метода к изучению экзотических состояний в ядрах с небольшим числом нуклонов. Полученные результаты демонстрируют возможность точного расчета энергий и свойств резонансных состояний непосредственно из первых принципов, без использования феноменологических потенциалов.

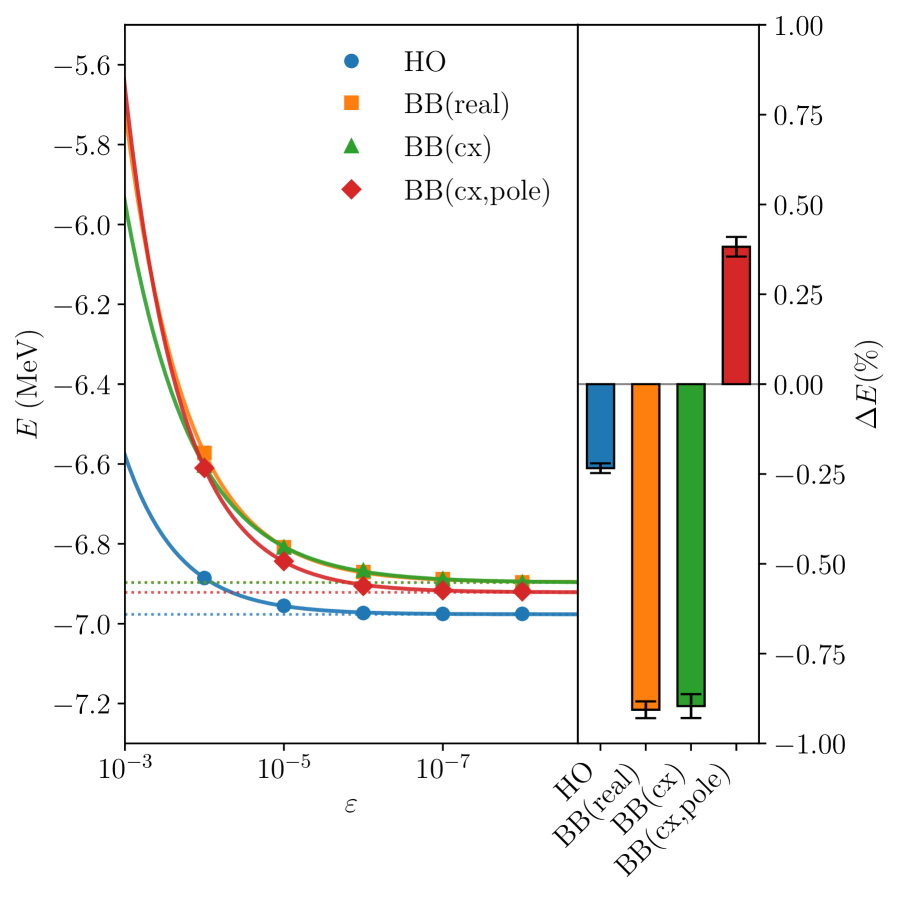
Энергия основного состояния <span class="katex-eq" data-katex-display="false"> \mathrm{He}_3 \mathrm{He} </span> вычисляется с помощью DMRG с различным уровнем усечения ε, при этом горизонтальные линии показывают экстраполированные значения, а относительная разница с точным результатом NCGSM представлена на правой панели в процентах. — Энергия основного состояния $\mathrm{He}_3 \mathrm{He}$ вычисляется с помощью DMRG с различным уровнем усечения ε, при этом горизонтальные линии показывают экстраполированные значения, а относительная разница с точным результатом NCGSM представлена на правой панели в процентах.

Валидация и Перспективы Развития

Результаты, полученные с использованием метода G-DMRG, прошли успешную валидацию посредством сравнения с расчетами, выполненными в рамках подхода NoCoreShellModel — NCGSM. Анализ показал, что расхождения между двумя методами не превышают 1% от результатов NCGSM, что подтверждает высокую точность и надежность G-DMRG. Такое соответствие является важным шагом в развитии методов расчета структуры атомных ядер, поскольку позволяет с уверенностью использовать G-DMRG для исследования более сложных систем и процессов, требующих высокой точности моделирования. Данная проверка обеспечивает прочную основу для дальнейшего применения метода в различных областях ядерной физики и астрофизики.

Данный метод опирается на фундаментальные принципы Ab Initio теории, что позволяет описывать атомные ядра, исходя исключительно из известных законов физики и свойств нуклонов. В основе расчетов лежит использование реалистичных ядерных взаимодействий, полученных в рамках $Chiral$ взаимодействия на уровне точности NNLOopt. Такой подход позволяет избежать эмпирических параметров и обеспечивает предсказательную силу, необходимую для понимания сложной структуры и поведения ядерной материи. Использование $Chiral$ взаимодействия обеспечивает согласованность с фундаментальными симметриями и позволяет точно моделировать ядерные силы, что критически важно для получения надежных результатов в расчетах структуры и реакций ядер.

Данное достижение открывает возможности для всестороннего и точного изучения структуры атомных ядер, протекающих в них реакций и процессов, происходящих в астрофизических условиях. Повышенная точность расчетов, основанная на $Ab Initio$ теории и реалистичных ядерных взаимодействиях, позволяет моделировать сложные ядерные системы с беспрецедентной детализацией. Это, в свою очередь, способствует углубленному пониманию механизмов синтеза элементов в звездах, процессов, определяющих стабильность ядер, и природы экзотических ядер, существующих лишь в экстремальных условиях. Возможность достоверного моделирования этих явлений имеет решающее значение для развития ядерной физики и смежных областей науки.

Перспективы развития метода G-DMRG связаны с расширением его применимости к более сложным и крупным системам. Исследователи намерены преодолеть существующие вычислительные ограничения, чтобы исследовать ядра с большим количеством нуклонов, что позволит получить более полное понимание их структуры и свойств. Кроме того, планируется изучение возможности применения G-DMRG к другим областям физики, выходящим за рамки ядерной физики, включая, например, физику конденсированного состояния и квантовую химию. Это расширение потенциально откроет новые возможности для моделирования и анализа сложных квантовых систем, способствуя прогрессу в различных областях науки и техники.

Для подтверждения работоспособности и высокой точности усовершенствованного кода G-DMRG, была проведена валидация с использованием ядра гелия-3 в качестве эталонной системы. Результаты расчетов для $³He$ продемонстрировали превосходное соответствие с теоретическими предсказаниями, подтверждая, что усовершенствованный алгоритм способен достоверно моделировать структуру и свойства легких ядер. Высокая степень согласования, достигнутая в процессе валидации, указывает на надежность метода и его применимость для дальнейших исследований более сложных ядерных систем и связанных с ними астрофизических процессов.

Исследование демонстрирует элегантность подхода к решению сложных задач ядерной физики. Авторы, оптимизируя пространство состояний и схемы усечения в методе G-DMRG, достигают впечатляющей точности в расчете широких многочастичных резонансов. Этот метод, позволяющий исследовать неустойчивые состояния ядер, требует тонкого баланса между вычислительной эффективностью и физической достоверностью. Как однажды заметил Карл Поппер: «Любая теория, которая не может быть опровергнута, не является научной». Именно стремление к фальсифицируемости, к постоянной проверке и усовершенствованию, лежит в основе представленной работы, где оптимизация базиса и процедур усечения направлена на минимизацию погрешностей и повышение надежности результатов. В этом кроется истинная красота научного поиска — не в достижении окончательных ответов, а в изящном процессе их приближения.

Что дальше?

Представленные усовершенствования в методе G-DMRG, несомненно, открывают новые возможности для исследования структуры и динамики ядерных резонансов. Однако, элегантность решения не должна заслонять остающиеся вопросы. Оптимизация базиса и процедур отсечения — это лишь приближение к истинной гармонии между формой и функцией. Подобно тонкой настройке инструмента, всегда остаётся пространство для улучшения, для достижения более точного и эффективного описания сложных многочастичных систем.

Будущие исследования неизбежно столкнутся с необходимостью преодоления ограничений, связанных с вычислительными ресурсами. Расширение применимости метода на более тяжёлые ядра — задача, требующая не только алгоритмических усовершенствований, но и более глубокого понимания фундаментальных принципов, управляющих ядерной материей. Истинный прогресс заключается не в увеличении масштаба вычислений, а в развитии более изящных и эффективных подходов.

В конечном итоге, цель состоит не в простом получении численных результатов, а в создании целостной картины ядерной структуры, где каждый элемент системы находится на своём месте, образуя гармоничное целое. Это требует не только технических инноваций, но и философского осмысления природы многочастичных взаимодействий, и, возможно, пересмотра некоторых устоявшихся представлений.

Оригинал статьи: https://arxiv.org/pdf/2601.16168.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-24 08:53