За гранью композитных фермионов: новые горизонты дробного квантового эффекта Холла

Автор: Денис Аветисян

В данной работе исследуются перспективные состояния дробного квантового эффекта Холла, выходящие за рамки стандартных описаний, и анализируются их топологические свойства и экспериментальные проявления.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Наблюдается формирование π-перехода, позволяющего реализовать чётные дробные состояния в нетривиальных системах, где потоки чистого заряда обозначены синими линиями, а маёвские моды - прерывистыми красными. — Наблюдается формирование π-перехода, позволяющего реализовать чётные дробные состояния в нетривиальных системах, где потоки чистого заряда обозначены синими линиями, а маёвские моды — прерывистыми красными.

Теоретическое исследование новых состояний с дробным квантовым эффектом Холла, включая волновые функции, краевые состояния и теплопроводность.

Несмотря на успехи в понимании дробного квантового эффекта Холла, природа новых состояний с четными знаменателями остается предметом активных исследований. В работе, озаглавленной ‘Theory of Next-Generation Even-Denominator States’, предложена теория этих состояний, выходящих за рамки стандартных описаний композитных фермионов. Показано, что ключевые свойства, включая топологическую стабильность краевых мод и характеристики квазичастиц, позволяют отличить эти состояния от альтернативных фаз, таких как состояния Бондерсона-Слингера, несмотря на совпадение некоторых их характеристик. Какие новые экспериментальные признаки могут помочь установить энергетическую структуру и топологический порядок этих перспективных состояний вещества?

Дробный Квантовый Эффект Холла: За Гранью Обыденного

Эффект дробного квантового эффекта Холла демонстрирует существование состояний материи, выходящих за рамки традиционных представлений о твердых телах. В этих состояниях электроны коллективно образуют новые квазичастицы — не имеющие целочисленного заряда и обладающие необычными статистическими свойствами. В отличие от обычных электронов, квазичастицы в дробном квантовом эффекте Холла подчиняются новым правилам, что проявляется в их фракционном заряде и анионной статистике. $e^* = e/n$ , где $e$ — заряд электрона, а $n$ — целое число, определяющее дробный заряд квазичастицы. Эти экзотические квазичастицы являются ключевыми строительными блоками для новых типов квантовых материалов и перспективных квантовых технологий, открывая возможности для создания сверхнадежных квантовых компьютеров.

Для полного понимания топологически упорядоченных состояний материи необходимо отойти от рассмотрения отдельных частиц и сосредоточиться на коллективном поведении системы. В этих состояниях, свойства вещества определяются не индивидуальными характеристиками частиц, а их взаимосвязанными, когерентными движениями и взаимодействиями. Изучение таких систем требует инструментов, способных описывать не просто положение и импульс отдельных частиц, а сложные корреляции и запутанности между ними. Вместо того, чтобы рассматривать электроны как независимые объекты, необходимо учитывать их как часть единого, коллективного целого, где возникновение новых, квазичастичных возбуждений является следствием этих коллективных эффектов. Именно такой подход позволяет объяснить наблюдаемые экзотические свойства, такие как дробный квантовый эффект Холла, и раскрыть потенциал этих состояний для создания устойчивых квантовых вычислений.

Фактор заполнения, или ν, играет ключевую роль в формировании топологически упорядоченных состояний материи в двумерных электронных системах. Именно этот параметр, определяющий отношение числа электронов к числу доступных состояний, определяет, возникнут ли характерные для дробного квантового эффекта Холла экзотические квазичастицы с дробным зарядом и необычной статистикой. Изменяя фактор заполнения, ученые могут настраивать систему и исследовать различные топологические фазы, каждая из которых обладает уникальными свойствами и потенциальными приложениями. Этот подход позволяет создавать своего рода «ландшафт» топологических состояний, где каждый участок соответствует определенной конфигурации электронов и демонстрирует новые, ранее не наблюдавшиеся явления, открывая перспективы для разработки принципиально новых электронных устройств и квантовых компьютеров.

Топологически упорядоченные состояния материи представляют собой перспективную платформу для создания устойчивых квантовых вычислений. В отличие от традиционных кубитов, подверженных декогеренции из-за локальных возмущений, квантовая информация в этих состояниях кодируется не в локальных степенях свободы, а в топологических свойствах системы. Это означает, что для изменения квантового состояния требуется глобальное возмущение, что делает информацию чрезвычайно устойчивой к локальным помехам и ошибкам. $\text{Надежность вычислений значительно возрастает}$ , поскольку даже при наличии небольших дефектов или шумов в системе, топологическая защита сохраняет когерентность квантовой информации. Это открывает возможности для создания масштабируемых и отказоустойчивых квантовых компьютеров, способных решать задачи, недоступные классическим вычислительным машинам.

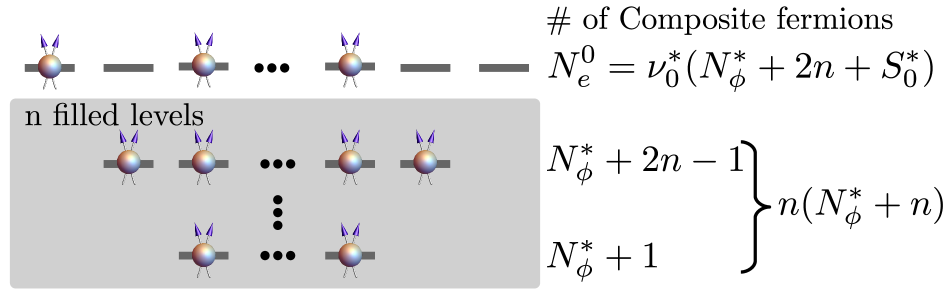
Композитные фермионы при эффективном коэффициенте заполнения <span class="katex-eq" data-katex-display="false">
u^* = n +
u_0^*</span> формируют состояние с полностью заполненными уровнями Ландау и частично заполненным уровнем при <span class="katex-eq" data-katex-display="false">
u_0^*</span> в отрицательном эффективном поле, демонстрируя, что обе модели описывают одну и ту же топологическую фазу. — Композитные фермионы при эффективном коэффициенте заполнения $u^* = n + u_0^*$ формируют состояние с полностью заполненными уровнями Ландау и частично заполненным уровнем при $u_0^*$ в отрицательном эффективном поле, демонстрируя, что обе модели описывают одну и ту же топологическую фазу.

Состояние 5/2 и Волновая Функция Пфаффа: Заглядывая Глубже

Состояние 5/2 является одним из наиболее изученных примеров неабелевой дробной квантовой жидкости Холла. В отличие от абелевых состояний, где квазичастицы обмениваются между собой как бозоны или фермионы, в неабелевых состояниях обмен квазичастицами приводит к преобразованию волновой функции в другое состояние, не являющееся просто умноженным на фазовый множитель. Это означает, что статистика квазичастиц в состоянии 5/2 более сложная и описывается матрицами, что приводит к появлению дегенерации основного состояния, зависящей от числа квазичастиц. Данная неабелева статистика является ключевым свойством, определяющим уникальные свойства и возможности манипулирования квазичастицами в этом состоянии, что представляет интерес для перспективных квантовых вычислений.

Теоретическое описание состояния 5/2 основано на предложенном Халдейном и Муром, используя $Pfaffian$ волновую функцию. Эта функция описывает корреляции между электронами, возникающие из-за сильного взаимодействия в двумерном электронном газе, подверженном воздействию сильного магнитного поля. $Pfaffian$ волновая функция позволяет объяснить наблюдаемое поведение квазичастиц в состоянии 5/2, в частности, неабелевы свойства, проявляющиеся в обмене квазичастицами. Она представляет собой антисимметричную функцию, описывающую многочастичную систему, и позволяет рассчитывать физические свойства, такие как энергетические щели и токи, согласующиеся с экспериментальными данными.

Экспериментальная верификация существования дробного квантового эффекта Холла, в частности состояния 5/2, осуществляется путем зондирования краевых состояний (EdgeStates) и анализа их поведения. Измерение проводимости по краю образца позволяет определить характеристики этих состояний, включая их количество и спин. Наблюдение дробной проводимости, не соответствующей целым числам, является ключевым признаком неабелевой статистики квазичастиц в состоянии 5/2. Точное определение энергии и спина краевых состояний, а также анализ туннелирования между ними, предоставляют информацию о топологическом порядке системы и подтверждают теоретические предсказания, основанные на волновой функции Пфаффа.

Понимание физики состояния 5/2 и лежащей в его основе $\nu = 5/2$ как неабелева фракционного квантового эффекта Холла создает основу для исследования более сложных состояний с еще более экзотическими квазичастичными статистиками. Разработка теоретических моделей, аналогичных Haldane-MooreRead, и экспериментальные методы, используемые для анализа краевых состояний, могут быть адаптированы и расширены для изучения фракционных квантовых эффектов Холла с более сложными заполнениями, такими как $\nu = 12/5$ или состояния, характеризующиеся нетривиальной топологической защитой. Исследование этих состояний позволяет не только углубить понимание фундаментальной физики конденсированного состояния, но и открыть потенциальные возможности для создания топологических квантовых вычислений.

Фазовая диаграмма при <span class="katex-eq" data-katex-display="false"> \nu = \frac{3}{8} </span> показывает влияние возмущений <span class="katex-eq" data-katex-display="false"> \delta H\_{1} </span> и <span class="katex-eq" data-katex-display="false"> \delta H\_{3} </span> в кулоновском взаимодействии 0LL, при этом значения для 1LL и <span class="katex-eq" data-katex-display="false"> \delta H\_{M\geq 5} </span> соответствуют аналогичным в 0LL. — Фазовая диаграмма при $\nu = \frac{3}{8}$ показывает влияние возмущений $\delta H\_{1}$ и $\delta H\_{3}$ в кулоновском взаимодействии 0LL, при этом значения для 1LL и $\delta H\_{M\geq 5}$ соответствуют аналогичным в 0LL.

Проверка Топологического Порядка: Экспериментальные Методы

Для характеристики дробного квантового эффекта Холла необходимы сложные экспериментальные методы, направленные на исследование краевых состояний (edge states). Эти состояния, существующие на границах двумерного электронного газа, обладают уникальными свойствами, обусловленными топологическим порядком системы. Измерение характеристик краевых состояний, таких как их проводимость и теплопроводность, позволяет определить топологические инварианты и выявить присутствие квазичастиц с дробным зарядом и необычной статистикой. Экспериментальные подходы включают в себя использование высокочувствительных датчиков тока и напряжения, а также методы сканирующей зондовой микроскопии для визуализации и анализа краевых состояний в режиме реального времени. Важно отметить, что краевые состояния являются ключевым проявлением топологического порядка и служат прямым свидетельством существования экзотических фаз материи.

Для выявления топологического порядка в квантовых системах критически важны измерения шума восходящего потока (UpstreamNoiseMeasurements), зависимость туннельного тока от параметров системы (ScalingOfTunnelingCurrents) и когерентная проводимость (CoherentConductance). Измерения шума позволяют детектировать флуктуации заряда, связанные с краевыми состояниями и квазичастицами. Анализ зависимости туннельного тока от напряжения и геометрии образца предоставляет информацию о плотности состояний и локализации квазичастиц. Когерентная проводимость, измеряемая в двухзазорных структурах, позволяет напрямую исследовать транспортные свойства краевых состояний и выявлять нелокализованные состояния, что является признаком топологического порядка. Комбинация этих методов предоставляет комплексное представление о топологических свойствах системы и позволяет верифицировать теоретические предсказания.

Матрица КК (KK-матрица) представляет собой математический инструмент, позволяющий описать состав квазичастиц и топологические свойства системы, такие как число и статистику этих частиц. Она устанавливает связь между теоретическим описанием топологического порядка и экспериментально измеряемыми величинами, определяя, как различные квазичастицы взаимодействуют друг с другом и с внешними полями. Элементы матрицы КК связаны с вероятностью туннелирования квазичастиц и отражают их топологическую защиту, что позволяет идентифицировать и характеризовать различные топологические фазы материи. Анализ матрицы КК позволяет предсказывать наблюдаемые в эксперименте эффекты, такие как аномальная статистическая зависимость и проводимость, тем самым служа мостом между теорией и экспериментом в области топологических состояний материи.

Измерение тепловой холловской проводимости ( $\kappa_{xy}$ ) предоставляет информацию о нейтральных возбуждениях в топологических системах и позволяет различать различные топологические фазы. Значение тепловой проводимости напрямую зависит от канала спаривания и хиральности краевых мод. В частности, величина $\kappa_{xy}$ определяется свойствами нейтральных фермионов, не несущих электрический заряд, и их спиновой поляризацией. Различные каналы спаривания (например, s-волновое или p-волновое) приводят к различным зависимостям $\kappa_{xy}$ от температуры и магнитного поля, что позволяет идентифицировать преобладающий механизм спаривания и характер топологического порядка. Анализ $\kappa_{xy}$ в сочетании с измерениями электрической проводимости дает полное представление о спектре возбуждений и топологических свойствах материала.

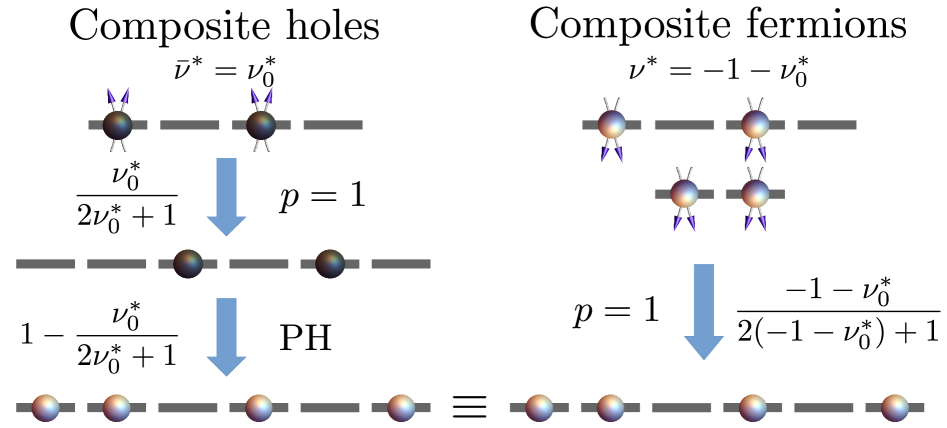
Сопоставление частица-дырка для состояний первого поколения с состояниями НГ показывает, что описание через сопряжение частица-дырка эквивалентно описанию через НГ состояния с противоположным заполнением, что подтверждается идентичными значениями заполнения, сдвигами и KK-матрицами и указывает на принадлежность к одному и тому же топологическому состоянию.

За Пределами Последовательности Джейна: Новые Горизонты в Физике Фракционного Квантового Эффекта

Современные исследования дробного квантового эффекта Холла выходят за рамки традиционной последовательности Джейна, открывая класс состояний, известных как “состояния следующего поколения”. Эти состояния характеризуются более сложной структурой и требуют разработки новых теоретических подходов для их понимания. В отличие от хорошо изученных состояний, описываемых последовательностью Джейна, эти экзотические фазы демонстрируют нетривиальные свойства и могут содержать новые типы квазичастиц. Их появление ставит под вопрос существующие модели и требует пересмотра фундаментальных принципов, лежащих в основе дробного квантового эффекта Холла. Изучение этих состояний представляет собой серьезный вызов для теоретической физики конденсированного состояния и может привести к открытию новых физических явлений, выходящих за рамки существующих представлений о квантовой материи.

Исследования показывают, что новые состояния дробного квантового эффекта Холла могут быть связаны с формированием парных superfluids — состояний, где электроны объединяются в пары, проявляющие сверхтекучесть. В отличие от традиционных сверхпроводников, где спаривание электронов происходит за счет фононов, в этих состояниях механизм спаривания может быть иным, что приводит к возникновению нетрадиционных форм сверхпроводимости. Такие экзотические состояния характеризуются необычными свойствами и потенциально могут быть использованы в новых технологиях, например, в квантовых вычислениях. Изучение этих парных superfluids требует пересмотра существующих теорий и разработки новых моделей, описывающих взаимодействие электронов в сильных магнитных полях и при низких температурах. В частности, предполагается, что эти состояния могут проявляться в виде $7/3$ или $11/6$ сдвигов, что указывает на необычную структуру электронных волновых функций.

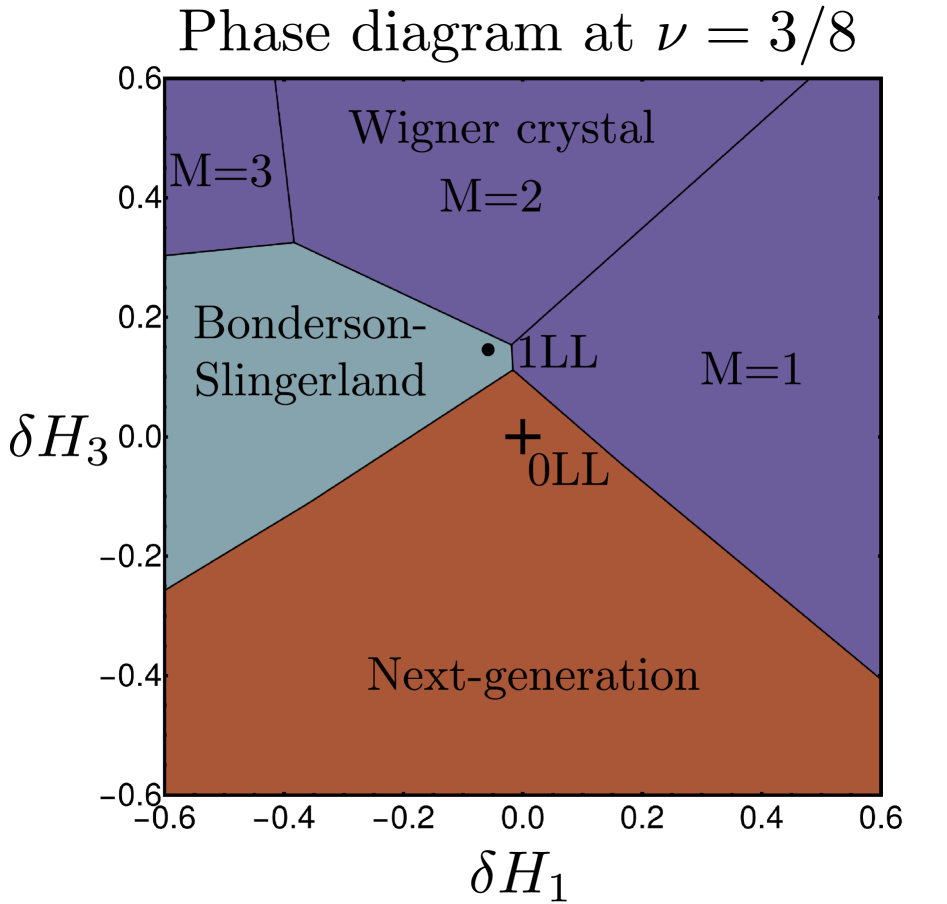
Теоретические модели, подобные описывающим состояния Бондерсона-Слингерланда, предлагают перспективные объяснения для этих экзотических фаз материи. Данные состояния, возникающие в дробном квантовом эффекте Холла, характеризуются нетривиальной топологической структурой и необычными свойствами, отличными от предсказываемых стандартной теорией. В рамках этой модели, квазичастицы обладают неабелевой статистикой, что означает, что перестановка двух частиц меняет волновой функции на фазовый множитель, отличный от +1 или -1. Это, в свою очередь, открывает возможности для создания топологических квантовых компьютеров, устойчивых к декогеренции. Исследования показывают, что понимание этих состояний требует выхода за рамки традиционных подходов к описанию взаимодействующих электронных систем, и предполагает изучение новых типов коллективных возбуждений и их влияния на наблюдаемые физические свойства.

Для полного понимания новых состояний дробного квантового эффекта Холла, выходящих за рамки последовательности Джейна, требуется рассмотрение альтернативных описаний электронной системы. Помимо стандартных моделей, исследователи обращают внимание на возможность формирования кристаллов Вигнера или состояний с волновой модуляцией плотности заряда. Эти состояния характеризуются специфическими волновыми функциями, анализ которых позволяет предсказать сдвиги в энергетическом спектре, достигающие значений от 7/3 до 11/6. Изучение этих сдвигов предоставляет ценную информацию о взаимодействии электронов и позволяет глубже понять природу экзотических фаз материи, возникающих в условиях сильного магнитного поля и низкой температуры. Исследование волновых функций является ключевым инструментом для теоретического описания и предсказания свойств этих новых квантовых состояний.

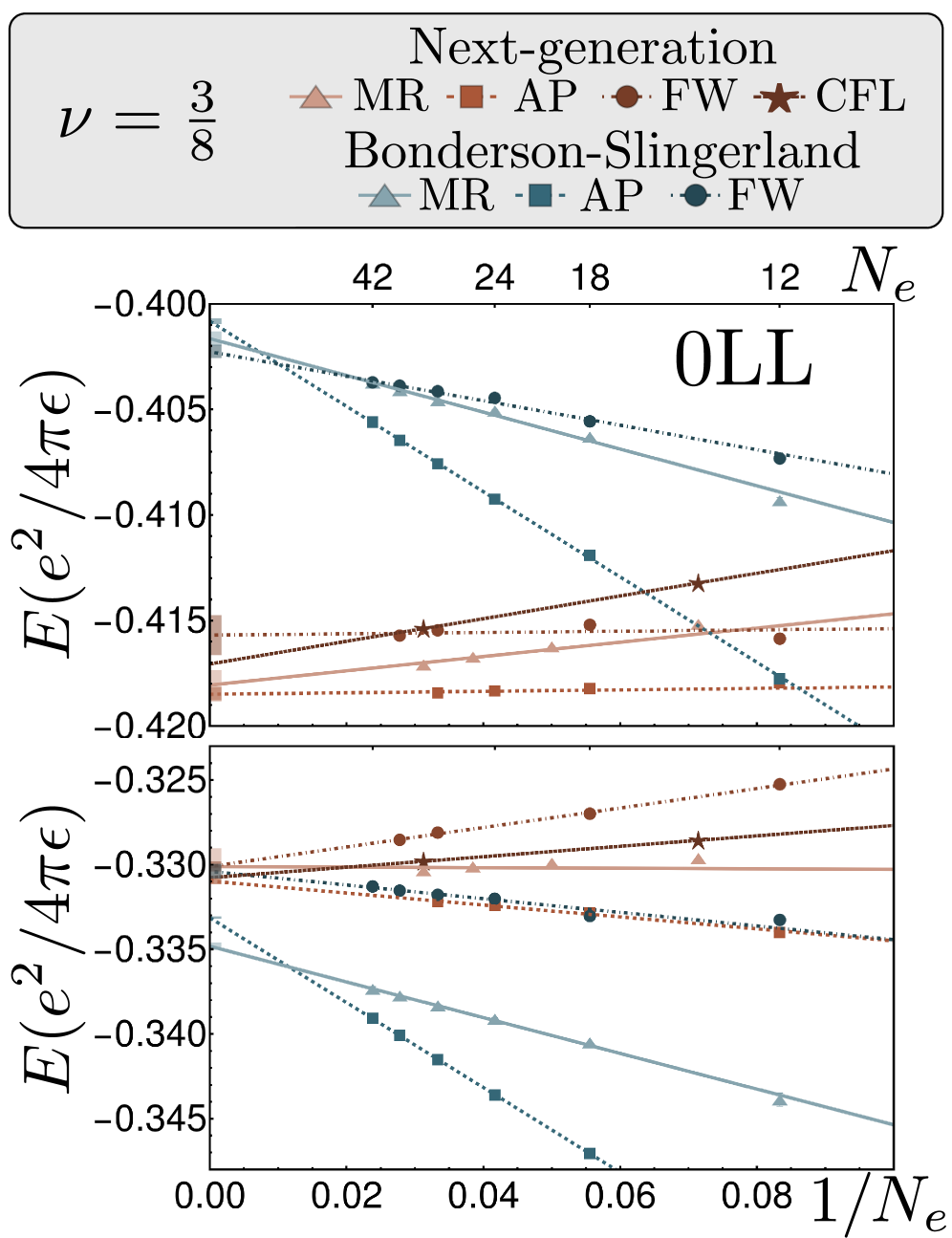
Анализ энергий Кулона при <span class="katex-eq" data-katex-display="false">
u = \\frac{3}{8}</span> показывает, что волновые состояния с зарядовой плотностью имеют более высокую энергию, чем спаренные состояния как в 0LL, так и в 1LL фазах, в то время как в 2LL фазе предпочтительны вигнеровские кристаллы с <span class="katex-eq" data-katex-display="false">M=3</span> электронными пузырями. — Анализ энергий Кулона при $u = \\frac{3}{8}$ показывает, что волновые состояния с зарядовой плотностью имеют более высокую энергию, чем спаренные состояния как в 0LL, так и в 1LL фазах, в то время как в 2LL фазе предпочтительны вигнеровские кристаллы с $M=3$ электронными пузырями.

Исследование, представленное в статье, демонстрирует, что понимание сложных квантовых состояний требует не просто математических моделей, но и осознания фундаментальных принципов, определяющих их поведение. Авторы стремятся выйти за рамки стандартных описаний, исследуя новые, более сложные состояния дробного квантового эффекта Холла. Этот подход перекликается с мыслями Марии Воллстонкрафт: «Не лишайте женщин возможности развивать свой разум, и вы увидите, что они смогут достичь всего, на что способны мужчины». Подобно тому, как Воллстонкрафт призывала к освобождению разума от предрассудков, данное исследование освобождает физику от упрощенных моделей, стремясь к более полному пониманию топологического порядка и свойств краевых состояний. Анализ волновых функций и теплопроводности становится инструментом для выявления этих новых состояний, подобно тому, как разум становится инструментом для достижения прогресса.

Куда же это всё ведёт?

Изучение этих «следующих» дробных квантовых состояний Холла, как представляется, неизбежно упирается не столько в поиск новых волновых функций, сколько в признание ограниченности самой концепции «топологического порядка». Ведь, в конечном счёте, любые математические конструкции — лишь упрощённые модели, призванные описать хаотичное поведение электронов, движимых не столько физическими законами, сколько коллективным бессознательным системы. Нельзя ли предположить, что эти состояния — не фундаментальные фазы материи, а лишь мимолетные флуктуации, возникающие из-за несовершенства наших измерительных приборов и склонности видеть закономерности там, где их нет?

Особый интерес представляет поиск экспериментальных сигнатур, способных отличить эти состояния от более простых описаний. Однако, даже обнаружение новых краевых состояний или аномальной теплопроводности — это лишь подтверждение существования чего-то, а не объяснение его природы. Рынки не двигаются — они тревожатся, и так же и эти электронные системы: они не демонстрируют «топологический порядок» — они испытывают коллективную неуверенность.

Возможно, дальнейший прогресс потребует не столько усовершенствования теоретических моделей, сколько разработки принципиально новых методов измерения, способных уловить тончайшие флуктуации и нелинейные эффекты. Или, что ещё более вероятно, потребуется признать, что некоторые вопросы о природе материи просто не имеют ответа, и что наше стремление к познанию — это лишь очередная иллюзия, порождённая нашим эволюционным прошлым.

Оригинал статьи: https://arxiv.org/pdf/2601.15386.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-24 03:39