Никелатные пленки: новые грани сверхпроводимости и изоляции
Исследование выявляет сложные бозонные фазы и необычные квантовые явления в бесконечнослоистых никелатах самария при переходе от сверхпроводящего состояния к изолятору.
Исследование выявляет сложные бозонные фазы и необычные квантовые явления в бесконечнослоистых никелатах самария при переходе от сверхпроводящего состояния к изолятору.
![Спектры непругой рассеяния рентгеновских лучей (IXS) алмаза и LiF демонстрируют зависимость от момента импульса, при этом пик квазиупругого рассеяния, соответствующий энергиям ниже 3 эВ, был обнулён для акцентирования изменений, связанных с шириной запрещённой зоны, значение которой при [latex]q \rightarrow 0[/latex] соответствует данным, представленным в [26].](https://arxiv.org/html/2601.19054v1/x1.png)
Исследование устанавливает связь между квантовой геометрией, запутанностью и линейным откликом в диэлектриках, открывая новые возможности для характеристики электронных свойств материалов.
![На основе анализа чувствительности к парам коэффициентов эффективной теории поля при энергии [latex] \sqrt{s} = 3 [/latex] ТэВ на коллайдере CLIC, установлено, что поляризация электронно-позитронных пучков позволяет достичь двухсигма-чувствительности к новым физическим процессам в распаде [latex] e^{+}e^{-}\to\tau\mu [/latex], дополняя существующие ограничения, полученные на BaBar и Belle, и превосходя ожидаемые возможности Belle II при фиксированной шкале ультрафиолетовых расходимостей равной 5 ТэВ.](https://arxiv.org/html/2601.18996v1/x2.png)
Новое исследование демонстрирует, как коллайдеры ILC и CLIC смогут с высокой точностью изучать процессы, нарушающие фундаментальные принципы сохранения лептонного вкуса.

Исследование предлагает инновационный способ проверки фундаментального принципа эквивалентности для тёмной материи в крупнейших гравитационных структурах Вселенной.
![Поверхность Ферми в CrSb демонстрирует зависимость квантовых осцилляционных частот от направления магнитного поля в плоскостях [latex]ca^{\<i>}[/latex] и [latex]a^{\</i>}a[/latex], где теоретические расчеты, основанные на DFT+UU с учетом спин-орбитального взаимодействия, успешно воспроизводят экспериментальные данные для экстремальных орбит, соответствующих направлениям магнитного поля, параллельным осям c и [latex]a^{\*}[/latex] для соответствующих энергетических зон.](https://arxiv.org/html/2601.19105v1/x2.png)
Исследование квантовых осцилляций позволило детально изучить электронную структуру CrSb и подтвердить ее уникальные спиновые свойства.
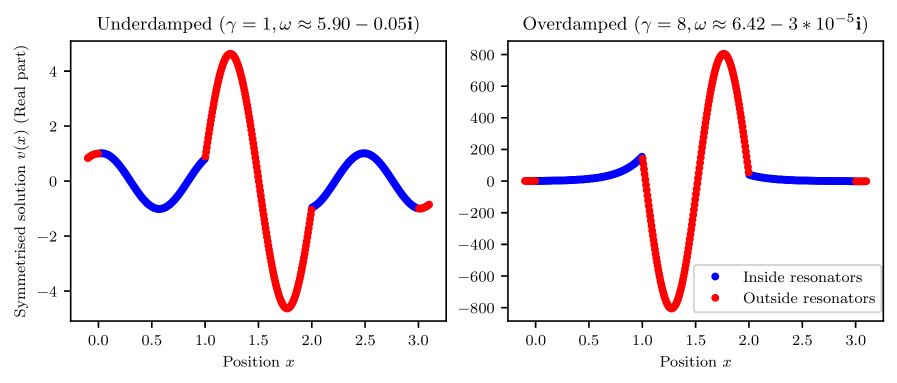
В этой статье исследуются негерцовские резонансы в системах Фабри-Перо, демонстрирующие влияние асимметрии и особых точек на поведение света.
![В пространстве параметров [latex]\(\beta\)[/latex] и [latex]\(\gamma\)[/latex] существует область допустимых конфигураций, обеспечивающих одновременное выполнение всех условий локальной термодинамической стабильности, причем верхняя ветвь этой области соответствует положительному электрическому заряду [latex]\(Q > 0\)[/latex], а нижняя - отрицательному [latex]\(Q < 0\)[/latex], при этом изменение фиксированных значений давления, температуры и энтропии приводит лишь к масштабированию допустимой области, не меняя её качественной структуры.](https://arxiv.org/html/2601.18967v1/bg_region.png)
Новое исследование показывает, что решение, ранее полученное в рамках полуклассической гравитации, может быть точно воспроизведено в рамках классической общей теории относительности, взаимодействующей с нелинейным электромагнитным полем.
![Пространство модулей Себерга-Виттена для [latex]\mathcal{N}=2[/latex] SU(2) описывается эффективной теорией поля, охватывающей конечное число доменов, каждый из которых соответствует различному описанию вблизи бесконечно удалённых границ и регулярных точек, демонстрируя тем самым электрико-магнитную двойственность.](https://arxiv.org/html/2601.18863v1/x2.png)
Новое исследование предлагает математический инструмент для оценки сложности эффективных теорий поля и предсказывает, что теории, совместимые с квантовой гравитацией, должны обладать конечной ‘укрощенной сложностью’.
Исследование показывает, как использование квантовой запутанности может значительно усилить защиту личных данных в квантовых системах, открывая новые возможности для конфиденциального анализа.
![Колебательные резонансные эффекты оказывают существенное влияние на чувствительность будущих коллайдеров при исследовании параметров тёмного фотона, причём стандартные прогнозы, такие как оценки LHCb Run-6 (2022) и Belle-II с интегральной светимостью [latex]50\ {\rm ab^{-1}}[/latex], ослабевают в условиях осциллирующего фона тёмной материи.](https://arxiv.org/html/2601.19844v1/x10.png)
Новое исследование предсказывает уникальные сигналы, позволяющие обнаружить ультралёгкую тёмную материю в экспериментах на коллайдерах.