![В исследовании модели Обри-Андре демонстрируется, что поведение системы, характеризуемое спектром и фазовой диаграммой класса CHU, выявляет масштабирование [latex]SQS\_Q[/latex] в зависимости от параметра λ, где при пересечении уровня Ферми полосы экспоненты масштабирования составляют 11, 0.618 и 2, а внутри запрещенной зоны - 2, при этом зависимость показателя ν от λ и энергии Ферми [latex]E\_F[/latex] указывает на диверсификацию при [latex]\lambda = 2[/latex] и формирует фазовую диаграмму, включающую классы гиперuniformности, отражающие влияние как классических, так и квантовых флуктуаций, при размере системы [latex]N = 17711[/latex].](https://arxiv.org/html/2601.18331v1/Fig1_newnew.png)
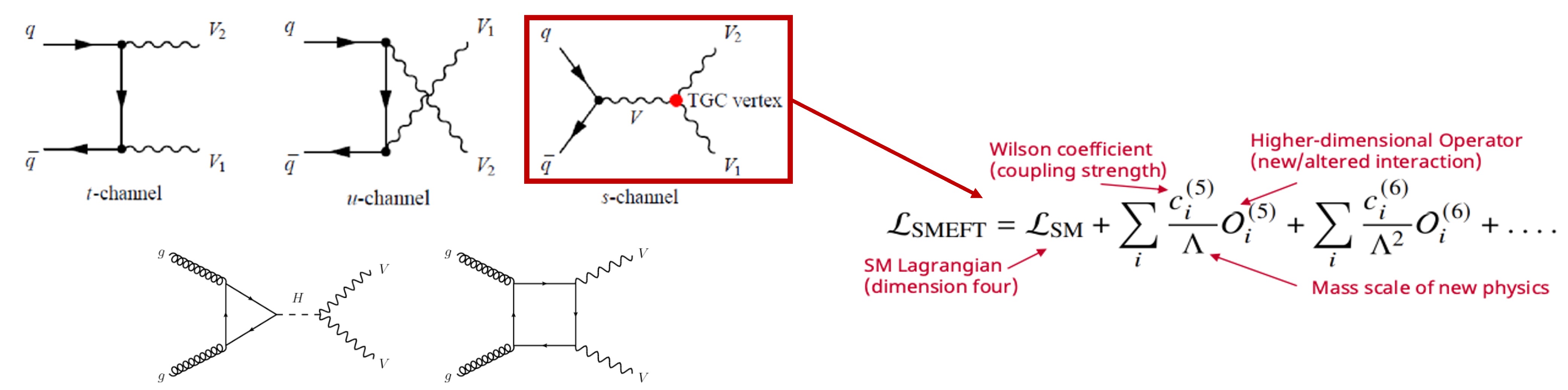
В статье представлена квантовая гиперравномерность как мощный инструмент для анализа квантовых состояний и фазовых переходов, позволяющий выявлять различные классы систем по степени подавления квантовых флуктуаций.
Новые результаты эксперимента ATLAS позволяют с высокой точностью проверить предсказания Стандартной модели и установить ограничения на эффекты, выходящие за её рамки.
Исследование посвящено изучению свойств плотной материи, содержащей странные кварки и гипероны, и ее влиянию на уравнение состояния в экстремальных условиях.
Новое исследование описывает процедуру калибровки и оценку неопределенностей в эксперименте ALPS II, предназначенном для поиска новых частиц за пределами Стандартной модели.
![Мнимый компонент псевдоэнтропии [latex] Sp_{AIS}^{I} [/latex] демонстрирует противоположные зависимости от [latex] \beta|\Delta| [/latex] при [latex] \beta = 10 [/latex], причём характер этой зависимости определяется знаком параметра анизотропии [latex] \Delta_{y} [/latex], что подтверждается анализом случаев [latex] \delta_{x} = 1, \delta_{y} = 0 [/latex] и [latex] \delta_{x} = -1, \delta_{y} = 1.1 [/latex].](https://arxiv.org/html/2601.17810v1/x2.png)
Исследование показывает, как энтропия квантовой спутанности во времени проявляется в условиях анизотропных пространств, проливая свет на природу времени в сильно взаимодействующих системах.
Исследование предлагает варианты модернизации экспериментальной установки ECN3 в CERN для расширения возможностей поиска гипотетических частиц, выходящих за рамки Стандартной модели.
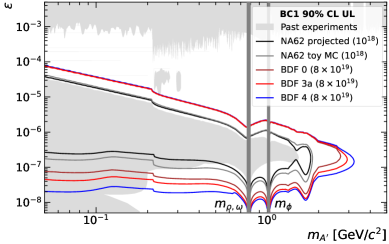
![В рамках анализа распада [latex]B^{+}\to K^{+}\nu\nu[/latex] и поиска новых физических эффектов, установлено, что операторы нарушения лептонного числа (LNV) способны подавлять первичную барионную асимметрию, при этом, ограничения, накладываемые распадом [latex]0\nu\beta\beta[/latex], и текущие границы распада [latex]B^{+}\to K^{+}\nu\nu[/latex] (синие линии) в сочетании с областями, соответствующими [latex]\eta_{B}=6.14\times 10^{-{10}}[/latex] (зеленые линии), позволяют оценить вклад операторов размерности 7 в объяснение массы нейтрино (красная линия), применительно ко второму сценарию, в то время как первый сценарий описывает поведение при изменении параметров [latex]C^{sb}_{\alpha\beta}[/latex].](https://arxiv.org/html/2601.16422v1/x4.png)
Новое исследование анализирует возможности обнаружения нарушений лептонного числа в редких распадах мезонов B и K, связывая их с фундаментальными проблемами космологии и физикой нейтрино.
Новая теоретическая модель предполагает, что гравитация может взаимодействовать с электрическим зарядом, приводя к различию в ускорении объектов с разным отношением заряда к массе.
![Для модели Эшкина-Теллера при граничных условиях [latex]A - h^z[/latex], конформные башни демонстрируют переходы уровней энергии при [latex]h^z = \pm \lambda[/latex], что подтверждается сравнением результатов, полученных методом DMRG для конечных размеров системы (фиолетовые, зеленые и синие символы), с экстраполированными результатами в термодинамическом пределе (красные круги), указывая на зависимость от параметра [latex]d\theta[/latex].](https://arxiv.org/html/2601.16951v1/x14.png)
Новое исследование раскрывает критические фазовые переходы и стабильные граничные условия в квантовой модели Ашкина-Теллера, используя передовые методы теории конформного поля и численного моделирования.
Новое исследование раскрывает уникальные свойства некомпланарных альтермагнитных систем, возникающих на специфической кристаллической решетке.