Квантовая нестабильность Тёмной Энергии: Пределы Квинтэссенции
Новое исследование показывает, что модели квинтэссенции, призванные объяснить тёмную энергию, могут быть подвержены фундаментальной нестабильности, связанной с ограничениями энтропии.
Наука
Новые грани полудираковских фермионов: влияние кулоновского взаимодействия
![В рамках расчетов на уровне Хартри-Фока для системы с [latex]g=1/2[/latex], эволюция показателя степени [latex]\eta(E)[/latex] в плотности состояний [latex]\rho(E) \sim E^{\eta(E)}[/latex] демонстрирует плавный переход от линейного дираковского поведения ([latex]\eta=1[/latex]) при низких энергиях к полудираковскому поведению типа II ([latex]\eta=1/3[/latex]) при увеличении энергии, что отражает изменение взаимодействующего спектра, представленное на рисунке 3, и зависит от силы взаимодействия α (0.05, 0.10, 0.20).](https://arxiv.org/html/2601.21098v1/x4.png)
Исследование показывает, как долгодействующие кулоновские взаимодействия изменяют свойства полудираковских фермионов, открывая возможности для контроля плотности состояний и других ключевых физических параметров.
Внутренний мир нуклона: новое понимание резонансов
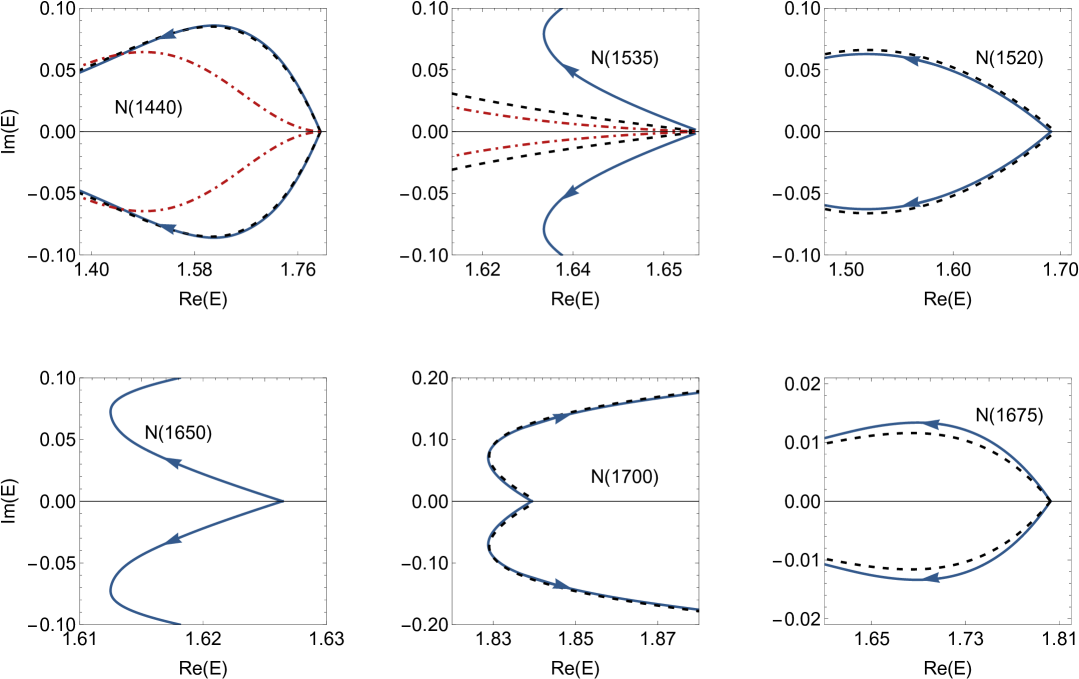
Исследование объединяет модель Ли-Фридрихса с процессами рождения кварковых пар для углубленного изучения свойств низкоэнергетических нуклонных резонансов.
Диамантовые дефекты под микроскопом: поиск sp³-связей
Новое исследование позволяет более точно идентифицировать sp³-связи на поверхности алмаза, используя комбинацию сканирующей туннельной спектроскопии и теоретического моделирования.
Предел чёрной дыры: нарушен ли третий закон?
![При решении типа (i) с [latex]A_k = 2k = 2g[/latex] наблюдается, что при [latex]V = 0[/latex] величина [latex]J[/latex] стремится к нулю, однако [latex]m_H[/latex] остается положительной, что указывает на специфическое поведение параметров Φ и [latex]\mathcal{B}[/latex] при приближении к пределу EMP.](https://arxiv.org/html/2601.20955v1/x2.png)
Новое исследование показывает, что в вакуумной гравитации возможно формирование экстремальных чёрных дыр, что ставит под сомнение один из фундаментальных принципов чёрной дыры.
Квантовая связь сквозь червоточины: новый взгляд на перенос информации
![В рассматриваемой конфигурации, характеризующейся параметрами [latex] (a,b,c,c) = (-8, -4, -{12}, 15) [/latex], локальный оператор, за счет индуцированной червоточиной запутанности, распространяет правящуюся моду в область BB (с незначительным влиянием на AA), при этом не оказывая влияния на левую моду, что приводит к увеличению запутанности SAS\_{A} и, как следствие, к положительному приросту взаимной информации ΔIAB>0.](https://arxiv.org/html/2601.21604v1/x9.png)
Исследование показывает, как запутанность может распространяться между двумя связанными квантовыми системами, имитируя перенос энергии и информации через теоретические туннели в пространстве-времени.
Поиск оптимальных форм: новый подход к геометрической оптимизации
![Оптимизированные множества точек, полученные с помощью FlowBoost, превосходят известные конструкции, демонстрируя расхождение в 0.073086 для [latex]N=20[/latex] и 0.032772 для [latex]N=60[/latex], при этом для [latex]N=20[/latex] их показатели приближаются к теоретическому оптимуму, доказанному в [18] и составляющему 0.0604.](https://arxiv.org/html/2601.18005v1/x35.png)
В статье представлена методика, использующая потоковые генеративные модели для эффективного решения сложных задач оптимизации, связанных с геометрией и поиском экстремальных значений.
Точная коррекция генома: новый инструмент для редактирования ДНК
[/latex], и иллюстрация закона Гаусса для одной из 11-формных симметрий [latex](103)[/latex], описываемая уравнением [latex](106)[/latex], демонстрируют, как применение оператора трансляции [latex]T\_x[/latex] к алгебре 11-формных диполей [latex](105)[/latex] с [latex]a\_{}b=x\_{}y[/latex] преобразует [latex]\mathcal{M}^{Z(1)}\_{xy,x}[/latex] в [latex]\mathcal{M}^{Z(1)}\_{xy,0}[/latex], подчеркивая внутреннюю структуру и динамику рассматриваемой системы.](https://arxiv.org/html/2601.21625v1/x7.png)
Исследователи разработали усовершенствованную систему редактирования оснований, позволяющую с высокой точностью преобразовывать аденин в гуанин в геноме человека.
Порядок из Хаоса: Новый Взгляд на Анализ Данных
Исследователи предлагают метод выявления фазовых переходов в данных рассеяния и изображений, не требующий предварительных физических моделей.
Поиск электрического дипольного момента электрона: новый рубеж с BaF
Исследование описывает передовой эксперимент по поиску электрического дипольного момента электрона с использованием молекул фторида бария, демонстрирующий текущую чувствительность и планы по дальнейшему улучшению.